Python: Binary Search / Bisection / Binary Search Tree (BST)

我先说下翻译的问题：

• bisection 是 “二等分” (指 action)，bisector 是 “二等分线”，这俩其实是几何的概念，不管你怎么引申，回溯到几何是最好理解的
• bisection method 是 “二分法”，是一系列使用 bisection 思想的方法的统称
• binary search 是 “二分查找”，这么翻译也行吧，我觉得英文的问题更大一点，叫 bisection search 不好么？
• binary search tree (BST) 是 “二叉搜索树”，从 tree 的角度而言，叫 binary 是 OK 的
  • 但是你 binary search 不能翻译成 “二叉搜索”，我们在搜索时没有 “叉” 这个动作

这一系列翻译我觉得最大的问题在 binary search，它应该叫 bisection search

1. Bisection in Geometry

几何学上的概念是简单的。比如我有一个 $x$-axis，或者直线 $(-\infty, +\infty)$，我在 $x=1$ 处切一刀，就做了一个 bisection，直线 $x=1$ 即是 bisector，如下图：

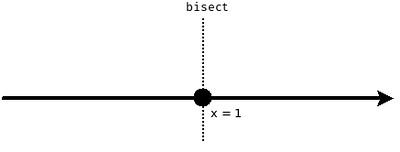
那在 python 有 bisect.bisect_left 和 bisect.bisect_right，为什么要分两个？它们有什么区别？

这是因为几何学不用考虑这个问题：$x=1$ 这个点，到底是属于左半边，还是右半边？(这肯定要涉及到度量) 但是你在实际应用中，比如我用在 array 上时，这个问题我必须要考虑。那这两个函数不严格地可以理解为：假设我在 $x=1$ 处有一个任意小的 neighborhood $\Phi(1, \epsilon)$，那么：

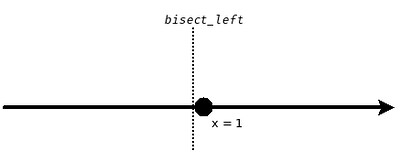
• bisect.bisect_left(X, 1) 就等价于 bisect X at the left boundary of (the neighborhood of) 1
  • 那么 $x=1$ 这个点就属于右半边
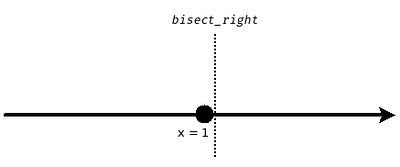
• bisect.bisect_right(X, 1) 就等价于 bisect X at the right boundary of (the neighborhood of) 1
  • 那么 $x=1$ 这个点就属于左半边

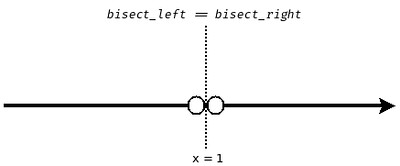
那从另外一个角度来说，如果直线上不存在 $x=1$ 这个点，比如说变成两条射线 $(-\infty, 1) \cup (1, +\infty)$，那么自然就不用管 $x=1$ 这个点的归属问题了。这个时候 bisect_left(X, 1) == bisect_right(X, 1)：

2. Bisection in Python

bisect.bisect_left 和 bisect.bisect_right 主要用来切 sequence，当然前提是假设 sequence 是 sorted (like an $x$-axis)。

那假设我有一个 sorted sequence a，我想在 value x 处切割 a，那么你 bisect_left(a, x) 和 bisect_right(a, x) 返回的其实是 a 中的一个 index，这个 index 标志了 bisector 在 a 中的位置。

我把参考实现 cpython/Lib/bisect.py 稍微修改了一下，如下：

def bisect_left(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        if a[mid] < x:  # ANCHOR
            lo = mid+1
        else: 
            hi = mid
    return lo

def bisect_right(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        if a[mid] <= x:  # ANCHOR
            lo = mid+1
        else: 
            hi = mid
    return lo

有点搞笑的是这两个函数在 cpython/Lib/bisect.py 的注释是一样的：

Return the index where to insert item x in list a, assuming a is sorted.

这 TM 完全没有抓住重点，而且你还引入了 insert 这个新概念来解释，简直是添乱。

其实这两个函数就只有一行是不同的，就是在注释 # ANCHOR 的地方，一个是 < 一个是 <=。

2.1 When x in a

可以看出，当 x in a 的时候：

• bisect_left 的 a[lo] 会停靠在 first occurrence of == x，然后一直走 else，让 hi 左移，往 lo 靠近
• bisect_right 如果一直有 a[mid] <= x，那么 lo 会一直右移，直到 first occurrence of > x，然后再是 hi 左移，往 lo 靠近

举个例子：

from bisect import bisect_left, bisect_right

a = [0, 1, 1, 1, 2]

i, j = bisect_left(a, 1), bisect_right(a, 1)
print(i, j)

# Output: 1 4

相当于就是：

a = [0, 1, 1, 1, 2]
        ^        ^
        i        j

那关于 slice 我们可以有一些结论。假设对同一个 x，i = bisect_left(a, x) 和 j = bisect_right(a, x)：

• $\forall e \in$ a[:i], $e < x$
• $\forall e \in$ a[i:], $e \geq x$
  • a[i] == x
• $\forall e \in$ a[:j], $e \leq x$
• $\forall e \in$ a[j:], $e > x$
  • a[j] > x
• $\forall e \in$ a[i:j], $e = x$

那 list 有个操作叫 lst.insert(index, value) 是说把 value 放到 lst[index]，然后后面的值全部往右 shift 一位。那么关于这个操作我们可以总结：

• a.insert(i, ?) inserts just before the leftmost x
• a.insert(j, ?) inserts just after the rightmost x
• 无论是 a.insert(i, 1) 还是 a.insert(j, 1) 可以把 1 放置到正确的地方并保持 a sorted

# after a.insert(i, ?)
a = [0, ?, 1, 1, 1, 2]
        ^        
        i      

# after a.insert(j, ?)
a = [0, 1, 1, 1, ?, 2]
                 ^
                 j 

然后有两个特殊情况要额外考虑一下：

1. a[0] == x 然后做 bisect_left(a, x) $\Rightarrow$ 会得到 i == 0
2. a[-1] == x 然后做 bisect_right(a, x) $\Rightarrow$ 会得到 j == len(a)

from bisect import bisect_left, bisect_right

a = [0, 1, 1, 1, 2]

i = bisect_left(a, 0)   # i == 0
j = bisect_right(a, 2)  # j == 5

a = [0, 1, 1, 1, 2] _
     ^              ^
     i              j

2.2 When x not in a

当 x not in a 的时候， # ANCHOR 的两句，if a[mid] < x 和 if a[mid] <= x 都会跨越到 first occurrence of > x，所以此时这两个函数是相同的逻辑，偏 bisect_right 的风格：

from bisect import bisect_left, bisect_right

a = [0, 0, 0, 0, 22]

i, j = bisect_left(a, 1), bisect_right(a, 1)
print(i, j)

# Output: 4 4

相当于就是：

a = [0, 0, 0, 0, 22]
                 ^^
                 ij

此时关于 slice 有：

• $\forall e \in$ a[:i], $e < x$
• $\forall e \in$ a[i:], $e > x$

关于 insert 有：

• a.insert(i, 1) 可以把 1 放置到正确的地方并保持 a sorted
• insert 之后一般都会有 a[i-1] < a[i] == 1 < a[i+1] (边界的特殊情况不考虑)

2.3 总结

无论我们有没有 x in a，我们似乎都可以说：

• bisect_left(a, x) returns the index of the last occurrence of < x plus 1
• bisect_right(a, x) returns the index of the first occurrence of > x

3. Binary Search

代码完全可以从 bisect_left 或者 bisect_right 引申而来，只需要加一个 condition 也就是 if a[mid] == x 单独处理一下就可以了：

def binary_search(a, x, lo=0, hi=None):
    if lo < 0:
        raise ValueError('lo must be non-negative')
    if hi is None:
        hi = len(a)
    while lo < hi:
        mid = (lo+hi)//2
        if a[mid] < x:
            lo = mid+1
        elif a[mid] == x:  # ANCHOR
            return mid
        else: 
            hi = mid
    return -1  # -1 is the error code if x not found in a

不同的实现，细节会不同，比如有初始化 hi = len(a) - 1 的，有 else: hi = mid - 1 的，这些都是边界的问题。我们这三个实现其实遵循了一个原则就是 lo 和 hi 组了一个半闭半开区间 [lo, hi)：在执行 while lo < hi 的时候，这个区间一直是合法的；当你 lo == high 的时候， [lo, high) 这个区间就坍缩了，此时 while 就要结束了。你也可以理解为当 a[lo:hi] 这个 slice 如果为空的时候，while 结束。

关于这个三个函数我想强调的是：

1. bisect module 并没有 提供 binary search 的接口
2. 在强假设 x in a 存在时，bisect_left(a, x) 碰巧 返回的是 the index of the first occurence of x，但它的逻辑 并不是 严格的 binary search

如果你坚持要用 bisect_left 来实现 binary search，可以这样：

from bisect import bisect_left

def binary_search(a, x):
    i = bisect_left(a, x)

    # bisect_left 不会 return -1
    if a[i] != x:
        return -1

    return i

4. A Subtle Bug in Above Code

参 Extra, Extra - Read All About It: Nearly All Binary Searches and Mergesorts are Broken。

问题主要是在 mid = (lo+hi)//2 这句。极端情况，如果你的 hi == 2**31 - 1 达到你 32-bit machine 的 int 的上限，那么这个加法 lo + hi 会 overflow。

改进很巧妙：

mid = lo + (hi - lo) // 2

5. Binary Search Tree (BST)

TBD