PWM (PSSM) / Sequence Logo

• PWM: Position Weight Matrix
• PSSM: Position-Specific Scoring Matrix

这俩其实是同一个概念，就是 motif 的 probabilistic representation。下面我们先从简单的 PFM 和 PPM 入手。

1. Motif Model / PFM: Position Frequency Matrix / PPM: Position Probability Matrix

首先看 RSA-tools: Introduction to cis-regulation 上的这个例子：

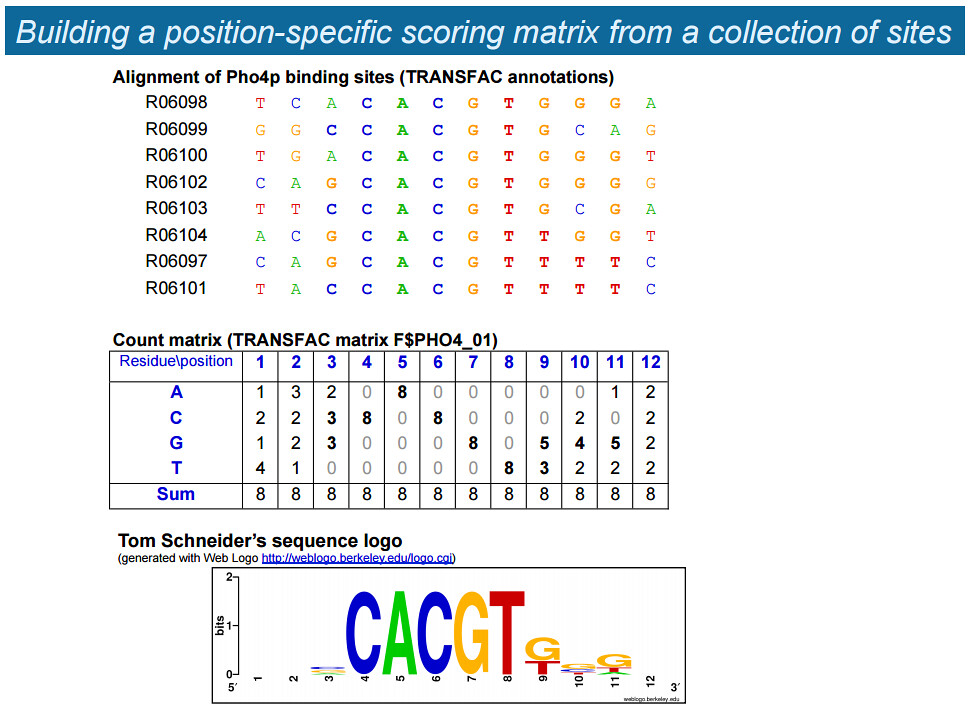
The TRANSFAC (TRANScription FACtor) database contains 8 binding sites for the yeast transcription factor Pho4p

• 5/8 contain the core of high-affinity binding sites (CACGTG)
• 3/8 contain the core of medium-affinity binding sites (CACGTT)

我们想根据这 8 个 TFBS 来制定它对应的 TFBM (Transcription Factor Binding Motif)。我们首先得到的这个 Count Matrix，其实就是 PFM (Position Frequency Matrix)。我们把每一个 cell 都除以 8，得到的就是 PPM (Position Probability Matrix):

\[M = { \begin{matrix} A \newline C \newline G \newline T \end{matrix}} {\begin{bmatrix} 0.125 & 0.375 & 0.25 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0.125 & 0.25\\ 0.25 & 0.25 & 0.375 & 1 & 0 & 1 & 0 & 0 & 0 & 0.25 & 0 & 0.25\\ 0.125 & 0.25 & 0.375 & 0 & 0 & 0 & 1 & 0 & 0.625 & 0.5 & 0.625 & 0.25\\ 0.5 & 0.125 & 0 & 0 & 0 & 0 & 0 & 1 & 0.375 & 0.25 & 0.25 & 0.25\\ \end{bmatrix} }\]

Both PPMs (and PWMs as well) assume statistical independence between positions in the pattern, as the probabilities for each position are calculated independently of other positions. Each column can therefore be regarded as an independent multinomial distribution (多项式分布).

我们称这个 $M$ 为 Motif Model。对任意一个长度为 12 的 sequence $x$，我们假定 “$x$ is a motif”，然后我们可以计算 “probability (likelihood) of $x$ given $M$”:

\[p(x|M) = \prod_{i=1}^{12} M_{x[i], i}\]

E.g. for $x = \text{TGACACGTGGGG}$,

\[\begin{aligned} p(x|M) &= 0.5 \times 0.25 \times 0.25 \times 1 \times 1 \times 1 \times 1 \times 1 \times 0.625 \times 0.5 \times 0.625 \times 0.5 \newline &= 0.00305175781 \end{aligned}\]

Pseudocounts (or Laplace estimators) are often applied when calculating PPMs if based on a small dataset, in order to avoid matrix entries having a value of 0.

• 原先是 $M_{I,i} = \frac{N(I)}{\sum_{I \in \lbrace A,C,T,G \rbrace}N(I)} = \frac{N(I)}{N(\text{sequence})}$
• 现在有 1st option: identically distributed pseudo-weight $k$
  • $M_{I,i}’ = \frac{N(I) + \frac{k}{4}}{N(\text{sequence})+k}$
• 2nd option: pseudo-weight distributed according to nucleotide priors
  • $M_{I,i}’ = \frac{N(I) + p(I)k}{N(\text{sequence})+k}$

2. Background Models (Genomic Context)

以下内容摘自 RSA-tools: Sequence models。

Why do we need a background model? Any motif discovery relies on an underlying model to estimate the random expectation. The choice of an inappropriate model can lead to false conclusions. In practice, a sequence model can be used to generate random sequences, which will serve to validate some theoretical assumptions.

What is the probability for a given sequence segment (oligonucleotide, “word”) to be found at a given position of a DNA sequence? Different models can be chosen. 我们称 background model 为 $B$。

2.1 Bernoulli Model

• Assumes independence between successive nucleotides.
• The probability of each nucleotide is fixed a priori
  • E.g. $p(A) = p(T) = 0.4$, $p(C) = p(G) = 0.1$
  • 对任意一个 sequence $x$，我们假定 “$x$ is a background sequence”，也就是说我们假定 “$x$ is not a motif”，然后我们可以计算 “probability (likelihood) of $x$ given $B$”
  • $p(x \vert B) = \prod_{i=1}^{\vert x \vert} p(x[i])$
• Particular case: equiprobable nucleotides
  • I.e. $p(A) = p(T) = p(C) = p(G) = 0.25$
  • Simple, but NOT realistic.
  • $p(x \vert B) = 0.25^{\vert x \vert}$

2.2 Markov Model

• The probability of each nucleotide depends on the $m$ preceding nucleotides.
• The parameter $m$ is called the order of the Markov model
• N.B. a Markov model of order 0 is a Bernoulli model.

2.2.1 Transition Matrix

• Each row specifies one prefix (the $m$ preceding nucleotides), each column one suffix (the current nucleotide).
• Each value is $p(x[i] \vert x[i-m:i])$

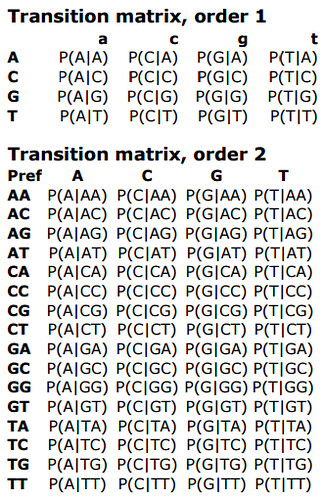
2.2.2 Model Estimation (Training)

这个 $p(x[i] \vert x[i-m:i])$ 如何 estimate？以 Order 1 的 $p(G \vert T)$ 为例：

\[p(G \vert T) = \frac{N(TG)}{N(TA) + N(TT) + N(TC) + N(TG)} = \frac{N(TG)}{N(T\ast)}\]

所以只要统计出 sequence collection 中所有 $2$-mer 的个数即可。

那么在 Markov model 下如何计算 $p(x \vert B)$ 呢？以下参考 Lecture 3: Probabilistic Sequence Models:

• 一般来说，$p(x \vert B) = p(x[1] \vert B) \times p(x[2] \vert x[1], B) \times \dots \times p(x[n] \vert x[1:n], B)$，其中 $\vert x \vert = n$
  • E.g. $p(ATCG \vert B) = p(A \vert B) \times p(T \vert A, B) \times p(C \vert AT, B) \times p(G \vert ATC, B)$
• 但是这样计算的工作量太大，我们这里使一个 trick：Markov Assumption
  • Assume the probability of a character is only dependent on the previous character, not the entire prefix
  • 这样就有 $p(x \vert B) = p(x[1] \vert B) \times p(x[2] \vert x[1], B) \times \dots \times p(x[n] \vert x[n-1], B)$，其中 $\vert x \vert = n$
    • E.g. $p(ATCG \vert B) = p(A \vert B) \times p(T \vert A, B) \times p(C \vert T, B) \times p(G \vert C, B)$
• A statistical process that uses Markov Assumption is called a Markov Chain.
• 这个 Assumption 还可以推广到 Order $m$:
  • $p(x \vert B) = p(x[1:m+1] \vert B) \prod_{i=m+1}^{\vert x \vert} p(x[i] \vert x[i-m:i], B)$

2.2.3 How to choose the sequence collection?

比如我们要 estimate the expected frequencies of length-$k$ yeast non-coding upstream sequences。我们可以选择的 sequence collection 可以有：

• whole yeast genome
  • But this will bias the estimates towards coding frequencies, especially in microbial organisms, where the majority of the genome is coding.
• whole set of yeast intergenic sequences
  • More accurate than whole-genome estimates, but still biased because intergenic sequences include both upstream and downstream sequences
• whole set of length-$k$ yeast upstream sequences
  • Requires a calibration for each sequence size
• whole set of upstream sequences, fixed size (default on the web site)
  • 意思说不管你 $k$ 是多少，我都给你提供一个固定的 length-$l$ 的 collection
  • Reasonably good estimate for microbes, NOT for higher organisms.

3. Position Weight Matrix

PWM 就是把 Motif Model $M’$ (经过 Pseudocounts 处理的 $M$) 的每一项除以 Bernoulli Model $B$ 中对应的 $p(I)$。PWM 不涉及 Markov model。

具体说来就是 $W_{I,i} = \ln \frac{M_{I,i}’}{p(I)}$，比如 $W_{A,1} = \ln \frac{M_{A,1}’}{p(A)}$

• $W_{I,i} > 0$ when $M_{I,i}’ > {p(I)}$, indicating $I$ in position $i$ is favorable of the motif
  • 在 TFBM 的问题中，$W_{I,i} > 0$ 说明 $i$ 位上有一个 $I$ 的话是容易被 TF 来 bind 的
• $W_{I,i} > 0$ when $M_{I,i}’ < {p(I)}$, indicating $I$ in position $i$ is unfavorable of the motif

对一个 sequence $x$，我们这样计算它的 Position Weight：$W_x = \sum_{i=1}^{\vert x \vert}W_{x[i], i}$。比如对 $x=CGTAAGGT$:

\[W_x = W_{C,1} + W_{G,2} + W_{T,3} + W_{A,4} + W_{A,5} + W_{G,6} + W_{G,7} + W_{T,8}\]

4. Sequence Logo

4.1 Shannon Entropy

Shannon Entropy is a measure of the uncertainty of a model, in the sense of how unpredictable a sequence generated from such a model would be.

For the single-nucleotide background model (i.e. Bernoulli model), the entropy is

\[H = -\sum_{I \in \lbrace A,C,T,G \rbrace} p(I) \log_2 p(I)\]

Similarly, we can then compute the entropy at each position $i$ of our motif model $M$:

\[H_i = -\sum_{I \in \lbrace A,C,T,G \rbrace} M_{I,i} \log_2 M_{I,i}\]

回到 background entropy。The maximum entropy of $B$ is reached when $p(A) = p(T) = p(C) = p(G) = \frac{1}{4}$:

\[H_{max} = - \Big ( \frac{1}{4} \log_2 \frac{1}{4} + \frac{1}{4} \log_2 \frac{1}{4} + \frac{1}{4} \log_2 \frac{1}{4} + \frac{1}{4} \log_2 \frac{1}{4} \Big ) = 2\]

When the logarithms are base 2, the units for such a quantity is called “bits”, as is with BLAST scores. When using natural logs, the units are “nits”. We can think of this value of 2 bits as the information content associated with knowing a particular nucleotide. A bit of information can also be understood as the number of questions necessary to unambiguously determine an unknown nucleotide. You could ask, “Is it a purine?” If the answer is “no”, you could then ask is it C? The answer to the second question always guarantees, non-canonical nucleotides aside, the nucleotide’s identity.

4.2 Information Content / Logo Height

注意我们说 Information Content 其实是 Motif 的 Information Content。

The Information Content of a motif at each position can be defined as the reduction in entropy. That is, the the motif provides information inasmuch as it reduces the uncertainty compared to the background model.

The Information Content of position $i$ is given by:

• For amino acids, $R_{i}=\log_{2}20-(H_{i} + e_{n})$
• For nucleic acids, $R_{i}=\log_{2}4-(H_{i} + e_{n})$
  • 这里 $\log_{2}4$ 就是上面的 $H_{max} = 2$
  • If $H_i = 0$, $R_i \rightarrow 2$:
    • No uncertainty at all: the nucleotide is completely specified (e.g. $p=\lbrace 1,0,0,0 \rbrace$)
  • If $H_i = 1$, $R_i \rightarrow 1$:
    • Uncertainty between two letters (e.g. $p=\lbrace 0.5,0,0,0.5 \rbrace$)
    • Need 1 extra bit to determine which nucleotide it is.
  • If $H_i = 2$, $R_i \rightarrow 0$:
    • Totally uncertainty ($p=\lbrace 0.25,0.25,0.25,0.25 \rbrace$)
    • 2 extra bits are required to specify a nucleotide in a 4-letter alphabet

The approximation for the small-sample correction, $e_{n}$, is given by:

\[e_{n}=\frac{1}{\ln 2} \times \frac{s-1}{2n}\]

where $s$ is 4 for nucleotides, 20 for amino acids, and $n$ is the number of sequences in the alignment (i.e. size of the sequence collection).

这个 $R_i$ 就是 Sequence Logo 第 $i$ 位的总高度。对第 $i$ 位上特定的一个 nucleotide $I$，它的高度是 $R_{I,i} = M_{I,i} \times R_i$。

• 高度越高，说明与 background model 的差异越大，越接近于 motif
• 高低越低，说明与 background model 的差异越小，越不可能是 motif