Closest Pair of Points
1. 问题
给定平面上的一个点集 $P = \lbrace p_1, \dots, p_n \rbrace$,求 Euclidean distance 最小的一对 $(p_i, p_j) \text{ where } p_i, p_j \in P$.
- 这个问题在天文 (星体距离)、民航等领域还是有很多应用的
本文参考 Sec 5.4, Algorithm Design by Jon Kleinberg etc. 且为了讨论的方便,我们不妨假设:no two points in $P$ have the same x-coordinate or the same y-coordinate.
2. 思路
2.1 大盘
brute force 能 $O(n^2)$,用 divide & conquer 能控制在 $O(n \log n)$.
那用 divide & conquer 无外乎这么个套路:
- 如果 $P$ 不用切分,进入 Trival Cases,直接算出最优解
- 如果 $P$ 需要切分,进入 Non-Trival Cases
- 切分 $P$,得到左半边和右半边 (sub-problems)
- 求得左半边内部的 cis-solution $\delta_{C1}$ 和右半边内部的 cis-solution $\delta_{C2}$
- 求得跨越左半边和右半边的一个 trans-solution $\delta_{T}$
- “cis-“ means “on the same side”
- “trans-“ means “on opposing sides”
- 求 $\min\lbrace \delta_{C1}, \delta_{C2}, \delta_{T} \rbrace$ 即是 $P$ 上的最优解
这题的难点就在于 $\delta_{T}$ 需要大量的数学证明,代码层面的难度其实并不大。
2.2 Trival Cases
- 如果点集 $P$ 只包含两个点,则直接计算它们的距离,作为这个点集 $P$ 上的局部最优解
- 如果点集 $P$ 只包含三个点,则逐对直接计算距离,取 min 作为这个点集 $P$ 上的局部最优解
2.3 Non-Trival Cases / 如何求 $\delta_{T}$
技术细节:How to Divide
我们可以把 $P$ 按 x-coordinate 排序,得到 $P_x$,然后取 mid point 做 split line $L$,划分成左半边的点集 $Q$ 和右半边的点集 $R$.
- 提前说一下:这题涉及的符号有点多,注意区分 “2D-space” 和 “set of points”
Lemma 1
假设我们已经把 $P$ 划分成左半边的点集 $Q$ 和右半边的点集 $R$,并求得了 $Q$ 上的 $\delta_{C1}$ 和 $R$ 上的 $\delta_{C2}$,我们取 $\delta = min(\delta_{C1}, \delta_{C2})$.
$Lemma\,1$: 假设存在跨越 $L$ 的最优解,即假设存在 point $q \in Q$ and point $r \in R$ 且 $d(q, r) < \delta$,那么 $q$ 和 $r$ 到 $L$ 的距离都不可能超过 $\delta$.
这么一来,我们可以限定在子空间 $B = \lbrace (x,y) \mid L - \delta \leq x \leq L + \delta \rbrace$ (可以理解为一个宽度为 $2 \times \delta$ 的 band) 内寻找 $\delta_{T}$.
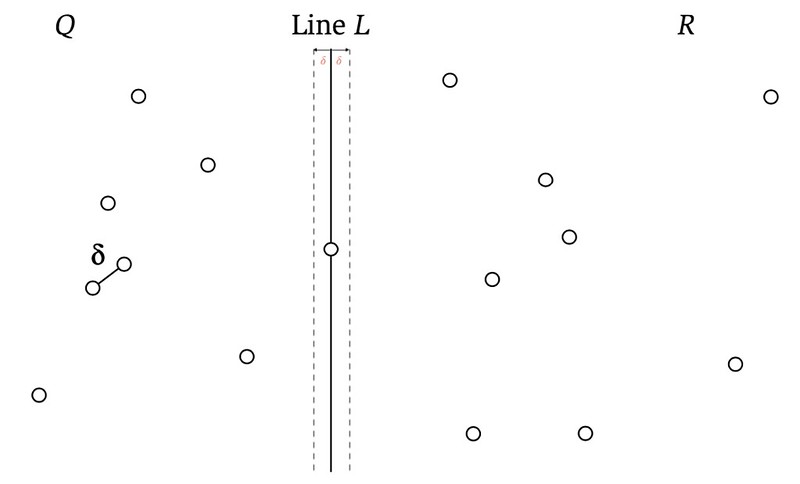
理论上,子空间 $B$ 内仍然可能有 $O(n)$ 个点,如果 brute force,最终仍然会上升到 $O(n^2)$. 此时我们需要 $Lemma\,2$.
Lemma 2
我们假设子空间 $B$ 上的点集为 $S$. 如果存在 $\delta_{T}$,它所对应的两个点 $s,s’ \in S$ 至要满足:
$Cond\,1$: $s$ 与 $s’$ 分居 $L$ 两侧- $Cond\,2$: $s$ 和 $s’$ 到 $L$ 的距离都不超过 $\delta$ ($Lemma\,1$)
- $Cond\,3$: $d(s, s’) < \delta$
可以看出:$Cond\,3$ implies $Cond\,1$ (如果同侧两个点满足 $Cond\,3$,那么 $\delta$ 一开始就不可能是 $\delta_{C1}$ 或者 $\delta_{C2}$),所以我们实际可以 discard $Cond\,1$.
我们考虑 $S$ 上的任意一个点 $s$. 我们给 $Lemma\,2$ 做这么一个 setup: 锚定 $s$ 的 y-coordinate (记作 $y_s$),以 $y=y_s$ 这条直线为 buttom line,则 $s$ 可以确定 $G(s) = \lbrace (x,y) \mid L - \delta \leq x \leq L + \delta, \, y_s \leq y \leq y_s + \delta \rbrace$ 这个一个 (矩形) 子空间。
在 $G(s)$ 上做长度为 $\frac{\delta}{2}$ 的 grid,可以用反证法证明 1 个 cell 内不可能有两个点。换言之,对任意的 $s$,它所决定的这个子空间 $G(s)$ 内至多只有 8 个点 (包括 $s$).
假设 $G(s)$ 内不包括 $s$ 的点集为 $Z(s)$,有 $| Z(s) | \leq 7$.
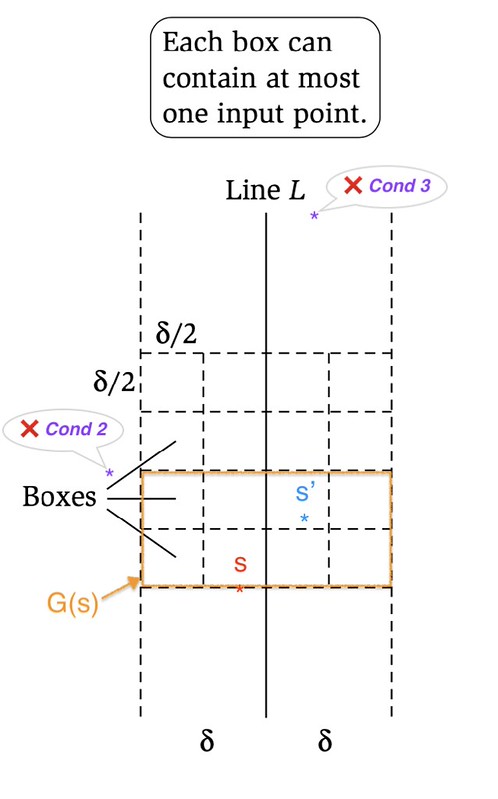
关键: $Z(s)$ 是 $s$ 以北空间内,能配合 $s$ 同时满足 $Cond\,2$ 和 $Cond\,3$ 的点 $s’$ 的超集
- $Z(s)$ 内的点一定满足 $Cond\,2$,可能满足但不一定满足 $Cond\,3$
- $Z(s)$ 以北的点一定无法满足 $Cond\,3$
- $Z(s)$ 以西、以东的点一定不满足 $Cond\,2$
所以求 $\delta_{T}$ 可以用这样的一个搜索过程:
def delta_T(S):
min_dist_list = []
for s in S:
eval(Z(s))
# cannot use s' as a variable name; use t instead
min_dist_from_s = min(d(s, t) for t in Z(s))
min_dist_list.append(min_dist_from_s)
return min(min_dist_list) # and later check if this value is less than delta
确定点集 $S$ 是容易的 (针对 $P$,用 band $B$ 做 x-axis 上的约束);但是给定 $s$,求 $Z(s)$ 是有点麻烦的。你可以用 $G(s)$ 去约束 $P$,但这需要遍历 $P$,也就是 $O(n)$,这会导致上述 delta_T 涨到 $O(n^2)$. $Lemma\,2$ 的作用就在于把求 $Z(s)$ 的消耗降到了 $O(1)$. 它是如何做到的呢?
因为我们已经确定了 $| Z(s) | \leq 7$,且 $y=y_s$ 这条直线为 buttom line,所以 $s$ 的 y-coordinate 比 $\forall s’ \in Z(s)$ 的 y-coordinate 都要小。如果我们把 $S$ 按 y-coordinate 排序,得到 $S_y$,且假设 $s \text{ is } S_y[i]$,那么 $Z_7(s) = \lbrace S_y[i+1], \dots, S_y[i+7] \rbrace$ 这 7 个点的集合一定会是 $Z(s)$ 的超集。首先使用超集来搜索对正确性没有影响;然后我们看下复杂度上的收益:
##############
## PREVIOUS ##
##############
def delta_T(S):
min_dist_list = []
for s in S: # O(n)
eval(Z(s)) # O(n)
min_dist_from_s = min(d(s, t) for t in Z(s)) # <= O(7)
min_dist_list.append(min_dist_from_s)
return min(min_dist_list)
# delta_T complexity: O(n^2)
###########
## AFTER ##
###########
def delta_T(S):
eval(Sy) from Py # O(n)
min_dist_list = []
for s in S: # O(n)
eval(Z7(s)) from Sy # O(7)
min_dist_from_s = min(d(s, t) for t in Z7(s)) # O(7)
min_dist_list.append(min_dist_from_s)
return min(min_dist_list)
# delta_T complexity: O(n)
最后,我们献上:
$Lemma\,2$: 假设存在两个点 $s,s’ \in S$ 且 $d(s, s’) < \delta$,那么 $s$ 和 $s’$ 在 $S_y$ 中的 index 差不会超过 7.
书上的这个常数是 15。虽然我们能看到它的 $G(s)$ 是一个 16-cell 的正方形 grid,但我实在没搞清楚它是如何 setup 的,我觉得我这个常数 7 的论述已经很 OK 了,就不深究了。
技术细节:如何高效计算 $Sy$
虽然我们定义 $Sy$ 是把 $S$ 上的点按 y-coordinate 排序后的结果,但你每次 delta_T 都 sort 一下其实不划算。
delta_T会执行 $O(\log_2 n)$ 次- 每次 sort
S理论上应该还是 $O(n \log n)$ - 合起来还是会到 $O(n^2)$
高效的做法是:
- 只做一次:把 $P$ 上的点按 y-coordinate 排序后,得到 $P_y$
- 用 band $B$ 约束 $P_y$,即可得到 $S_y$
- 这个过程只需要遍历一次 $P_y$,是 $O(n)$
- 所以执行 $O(\log_2 n)$ 次
delta_T,总的开销还是 $O(n \log n)$
3. 代码
我觉得这个题目拿来面试的话难度太大了,所以干脆就写得偏 OO 一点,方便理解。
3.1 Band / 点 / 点集
真的把 “点集” 实现成一个 set 似乎并不明智,所以我们用自定义集合类 PointList 来表示。(Is this a Composite Pattern?)
import math
from operator import attrgetter
class Band:
def __init__(self, x_min, x_max):
self.x_min = -math.inf if x_min is None else x_min
self.x_max = math.inf if x_max is None else x_max
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def __eq__(self, other): # cannot use type hint `other: Point` here
if not isinstance(other, Point):
return NotImplemented # this is a best practice for __eq__, instead of raising errors
return self.coord == other.coord
def __hash__(self):
return hash(self.x) ^ hash(self.y) # learned from Fluent Python
@property
def coord(self):
return (self.x, self.y)
def inside(self, b: Band):
return b.x_min <= self.x <= b.x_max
class PointList:
def __init__(self, points: list):
self.points = points
def __len__(self):
return len(self.points)
def __getitem__(self, index):
return self.points[index]
def sorted(self, key):
sorted_points = sorted(self.points, key=attrgetter(key))
return PointList(list(sorted_points))
def subset(self, b:Band):
inside_points = [p for p in self.points if p.inside(b)]
return PointList(inside_points)
3.2 单独给 “解” 这个概念定一个类
from scipy.spatial.distance import euclidean
class Solution:
def __init__(self, p: Point, q: Point):
self.p = p
self.q = q
self.distance = euclidean(p.coord, q.coord)
def __eq__(self, other):
if not isinstance(other, Solution):
return NotImplemented
return self.distance == other.distance
def __lt__(self, other):
if not isinstance(other, Solution):
return NotImplemented
return self.distance < other.distance
def __str__(self):
return f"distance={self.distance}, from={self.p.coord}, to={self.q.coord}"
3.3 divide & conquer
def closest_pair_main(p_list: PointList):
px_list = p_list.sorted(key='x')
py_list = p_list.sorted(key='y')
return closest_pair_of_points(px_list, py_list)
def closest_pair_of_points(px_list: PointList, py_list: PointList):
# it is possible that len(px_list) != len(py_list)
if len(px_list) < 2:
raise ValueError(f"Need at least 2 points to calculate. Got {len(p_list)} points.")
if len(px_list) == 2:
return Solution(p_list[0], p_list[1])
if len(px_list) == 3:
return min(Solution(px_list[0], px_list[1]),
Solution(px_list[0], px_list[2]),
Solution(px_list[1], px_list[2]))
"""
假设 n = len(p_list)
0 ... mid_index, mid_index + 1, ..., n-1
--------------- -----------------------
left half right half
n 为偶数时,left half 与 right half 等长
n 为奇数时,left half 比 right half 多一个元素
这么划分是因为我想把 px_list[mid_index] 定为 L 穿过的点
"""
mid_index = (len(px_list) + 1) // 2 - 1
# cis- means "on the same side"; trans- means "on opposing sides"
# it's a pity that I cannot subset py_list here...
cis_solution_left = closest_pair_of_points(px_list[:mid_index+1], py_list)
cis_solution_right = closest_pair_of_points(px_list[mid_index+1:], py_list)
cis_solution = min(cis_solution_left, cis_solution_right)
l = px_list[mid_index].x # the split line L
delta = cis_solution.distance
trans_solution = closest_pair_of_trans_points(py_list, l, delta)
return min(cis_solution, trans_solution)
def closest_pair_of_trans_points(py_list: PointList, l, delta):
B = Band(x_min=l-delta, x_max=l+delta)
# 没有必要算 S,直接拿 Sy 遍历是一样的
Sy = py_list.subset(B)
n = len(Sy)
solutions = [None] * (n-1) # 最后一个点 Sy[-1] 的 Z 为空,不需要计算
for i in range(n-1):
s = Sy[i]
Z = Sy[i+1 : max(i+8, n)]
solutions[i] = min(Solution(s, t) for t in Z)
return min(solutions)
3.4 Test Cases
Credit to Closest Pair Implemetation Python.
p_coords = [(0,0),(7,6),(2,20),(12,5),(16,16),(5,8),(19,7),(14,22),(8,19),(7,29),(10,11),(1,13)]
p_list = PointList([Point(*c) for c in p_coords])
# distance=2.8284271247461903, from=(5, 8), to=(7, 6)
print(closest_pair_main(p_list))
p_coords = [(94, 5), (96, -79), (20, 73), (8, -50), (78, 2), (100, 63), (-14, -69), (99, -8), (-11, -7), (-78, -46)]
p_list = PointList([Point(*c) for c in p_coords])
# distance=13.92838827718412, from=(99, -8), to=(94, 5)
print(closest_pair_main(p_list))
留下评论