5 minute read

1. Generative vs Discriminative

参考 Mihaela van der Schaar: Generative vs. Discriminative Models, Maximum Likelihood Estimation, Mixture Models:

  • Generative Model $\Rightarrow$ tries to learn $\mathbb{P}_{\mathbf{Y}, \mathbf{X}}(y, \mathbf{x})$
    • 这两条路线都可以走：
      • $\mathbb{P}_{\mathbf{Y}, \mathbf{X}}(y, \mathbf{x}) = \mathbb{P}_{\mathbf{Y} \vert \mathbf{X}}(y \vert \mathbf{x}) \, \mathbb{P}_{\mathbf{X}}(\mathbf{x})$
      • $\mathbb{P}_{\mathbf{Y}, \mathbf{X}}(y, \mathbf{x}) = \mathbb{P}_{\mathbf{X} \vert \mathbf{Y}}(\mathbf{x} \vert y) \, \mathbb{P}_{\mathbf{Y}}(y)$
    • Explicitly models the distribution of both the features and the corresponding labels (classes)
    • Aims to explain the generation of all data
    • Example techniques:
      • Naive Bayes Classifier
      • Hidden Markov Models (HMM)
      • Gaussian Mixture Models (GMM)
      • Multinomial Mixture Models
  • Discriminative Model $\Rightarrow$ tries to learn $\mathbb{P}_{\mathbf{Y} \vert \mathbf{X}}(y \vert \mathbf{x})$
    • Aims to predict relevant data
    • Example techniques:
      • $K$ nearest neighbors
      • logistic regression
      • linear regression
        • 没错，linear regression 其实是 discriminative model
        • 我觉得这就是 discriminative 这个名字不好的地方
      • Conditional Random Fields (CRFs)
        • Logistic Regression is the simplest CRF
      • SVMs
      • perceptrons

2. Frequentist vs Bayesian

Section 5.6 Bayesian Statistics, Deep Learning 上说：

As discussed in section 5.4.1, the frequentist perspective is that the true parameter value $\theta^\ast$ is fixed but unknown, while the point estimate $\hat{\Theta}_m$ is a random variable on account of it being a function of the dataset (which is seen as random).

The Bayesian perspective on statistics is quite different. The Bayesian uses probability to reflect degrees of certainty of states of knowledge. The dataset is directly observed and so is not random. On the other hand, the true parameter $\theta^\ast$ is unknown or uncertain and thus is represented as a random variable.

但是，从我找到的其他材料，以及 Deep Learning 后面自己的 Example: Bayesian Linear Regression 小节来看，我并没有看出 Bayesian machine learning 在 model 的时候有把 (training) dataset 看做 observed。所以我觉得 Frequentist vs Bayesian machine learning 最大的一点区别就在于：

  • Frequentist $\Rightarrow$ the true, unknown parameter $\theta^\ast$ is a value
    • 所以 Frequentist machine learning $\Rightarrow \mathbb{P}_{\mathbf{D}}(\mathbf{d}; \theta)$
      • $\theta$ is not modeled probabilistically
  • Bayesian $\Rightarrow$ the true, unknown parameter $\theta^\ast$ is a random variable
    • 所以 Bayesian machine learning $\Rightarrow \mathbb{P}_{\mathbf{D}, \Theta}(\mathbf{d}, \theta)$
      • $\theta$ is modeled probabilistically
    • 这个 $\theta$ 可以是 latent variable

具体处理起来的话，一般的做法是：

  • Frequentist $\Rightarrow$
    • 写出 $\mathbb{P}_{\mathbf{D}}(\mathbf{D}; \theta) = \prod_{i=1}^{m}\mathbb{P}_{D_i}(\mathbf{d}_i; \theta)$ 的表达式
    • 做 point estimate $\hat{\theta} \to \theta^\ast$ 使得 $\mathbb{P}_{\mathbf{D}}(\theta) \to \mathbb{P}_{\mathbf{D}}^\ast$
    • 对 test data 做 prediction：$\mathbf{d}_{m+1} = \mathbb{E}[\mathbb{P}_{D_{m+1}}(\mathbf{d}_{m+1}; \hat{\theta})]$
  • Bayesian $\Rightarrow$
    • 变形 $\mathbb{P}_{\Theta \vert \mathbf{D}}(\theta \vert \mathbf{D}) = \frac{\mathbb{P}_{\mathbf{D} \vert \Theta}(\mathbf{D} \vert \theta) \, \mathbb{P}_{\Theta}(\theta)}{\mathbb{P}_{\mathbf{D}}(\mathbf{D})}$
      • 或者用 $\mathbb{P}_{\Theta \vert \mathbf{D}}(\theta \vert \mathbf{D}) \propto \mathbb{P}_{\mathbf{D} \vert \Theta}(\mathbf{D} \vert \theta) \, \mathbb{P}_{\Theta}(\theta)$ 做 MAP
      • 注意：做 MAP 会让人觉得这很像是 Frequentist，但注意 Bayesian 的主要特征其实是变形
    • 对 test data 做 prediction：$\mathbb{P}(D_{m+1} \vert \mathbf{D}) = \int \mathbb{P}(D_{m+1} \vert \theta) \, \mathbb{P}(\theta \vert \mathbf{D}) d\theta$
      • 可以得到 $D_{m+1} \vert \mathbf{D}$ 的 distribution

注意这里的 $\mathbf{D} = \lbrace D_1, \dots, D_m \rbrace$ 表示 (training) dataset，看做是 1 个 sample、$m$ 个 random variable。$D_i$ realized 得到一个具体的 data point $\mathbf{d}_i$。非常重要的一点：

  • 这个 $\mathbf{D}$，它既可以表示 $\mathbf{D} = \mathbf{Y}, \mathbf{X}$，也可以表示 $\mathbf{D} = \mathbf{Y} \vert \mathbf{X}$，完全看你自己的需求
  • 也就是说：无论是 Frequentist 还是 Bayesian machine learning，$\mathbf{D}$ 的形式确定了你到底是 Generative 还是 Discriminative model

3. Generative vs Discriminative, Frequentist vs Bayesian

所以这两种划分是不冲突的，我们完全可以做一个 $2 \times 2$ 的 table (参考 Generative vs. Discriminative; Bayesian vs. Frequentist)：

  Frequentist Bayesian
Discriminative $\mathbb{P}_{\mathbf{Y} \vert \mathbf{X}}(y \vert \mathbf{x}; \theta)$ $\mathbb{P}_{(\mathbf{Y} \vert \mathbf{X}), \Theta}\big( (y \vert \mathbf{x}), \theta \big)$
Generative $\mathbb{P}_{\mathbf{Y}, \mathbf{X}}(y, \mathbf{x}; \theta)$ $\mathbb{P}_{\mathbf{Y}, \mathbf{X}, \Theta}(y, \mathbf{x}, \theta)$
  • Items to the right of the semicolon (;) are not modeled probabilistically
  • 注意符号：
    • $\mathbb{P}_{\mathbf{Y} \vert \mathbf{X}, \Theta}$ 表示 “distribution of $\mathbf{Y}$, conditioned on $\mathbf{X}$ and $\Theta$”
    • $\mathbb{P}_{(\mathbf{Y} \vert \mathbf{X}), \Theta}$ 表示 “joint distribution of $\mathbf{Y} \vert \mathbf{X}$ and $\theta$”

4. Unsupervised vs Supervised

明显可以看出，无论是 generative 还是 discriminative，它们都是 supervised learning 的范畴，因为它们都有 $\mathbf{Y}$。

那么 unsupervised learning 我们可以简单理解为去 learn $\mathbb{P}_{\mathbf{X}}(\mathbf{x})$ 吗？不一定。

首先，density estimation $\mathbb{P}_{\mathbf{X}}(\mathbf{x})$ 的确算是 unsupervised learning 的范畴，但其实还有很多的 unsupervised learning 是 $\mathbb{P}_{\mathbf{K} \vert \mathbf{X}}(\mathbf{k} \vert \mathbf{x})$ 的形式，比如：

  • clustering 可以看做是 learn $\mathbb{P}_{\mathbf{C} \vert \mathbf{X}}(c \vert \mathbf{x})$
  • PCA 可以看做是 learn $\mathbb{P}_{\mathbf{X’} \vert \mathbf{X}}(\mathbf{x}’ \vert \mathbf{x})$
  • embedding 可以看做是 learn $\mathbb{P}_{\mathbf{E} \vert \mathbf{X}}(\mathbf{e} \vert \mathbf{x})$

回到 Frequentist vs Bayesian 的讨论。那我们其实也可以让 $\mathbf{D} = \mathbf{X}$ 或者 $\mathbf{D} = \mathbf{K} \vert \mathbf{X}$ (虽然一开始 $\mathbf{K}$ 未知)，这么一来也可以有 Frequentist unsupervised learning 和 Bayesian unsupervised learning

5. Frequentist Discriminative Example: Linear Regression

我们之前在 Terminology Recap: Sampling / Sample / Sample Space / Experiment / Statistical Model / Statistic / Estimator / Empirical Distribution / Likelihood / Estimation and Machine Learning 有说：

  • MLE 等价于 minimizing KL divergence $D_{KL}(\hat{\mathbb{P}}_{\text{data}} \Vert \mathbb{P}_{\text{model}})$
  • MLE 等价于 minimizing cross-entropy $H(\hat{\mathbb{P}}_{\text{data}}, \mathbb{P}_{\text{model}})$
    • When $\mathbb{P}_{\text{model}}$ is Gaussian，等价于 minimizing $\operatorname{MSE}$
    • 亦即 $\operatorname{MSE}$ is the cross-entropy between the empirical distribution and a Gaussian model.

linear regression 并没有说需要 assumption on Gaussian distributions，但是你会注意到我们 linear regression 一般是 minimizing $\operatorname{MSE}$，联系我们之前说到的 “$\operatorname{MSE}$ is the cross-entropy between the empirical distribution and a Gaussian model”，那么 linear regression 中到底哪里出现了 Gaussian model 呢？

We can imagine that with an infinitely large training set, we might see several training examples with the same input value $\mathbf{x}$ but different values of $y$. 那我们假设单个 input $\mathbf{x}_1$ 对应的所有 output 构成一个 sample $Y_1$，你的 training data $y_1$ 只是 $Y_1$ 的一个 value；我们假设 $Y_1 \vert \mathbf{x}_1 \sim \mathcal{N}(?, ?)$ (这是我们在 $\mathbf{x}_1$ 处的 $\mathbb{P}_\text{model}$)

根据 linear regression 的 assumption，$Y_1 = \mathbf{w} \mathbf{x}_1 + \epsilon$，然后 $\epsilon$ 是 Bayes error，所以假设有 $\epsilon \sim \mathcal{N}(0, \sigma^2)$，所以有：

\[\begin{aligned} \mathbb{E}[Y_1] &= \mathbb{E}[\mathbf{w} \mathbf{x}_1] + \mathbb{E}[\epsilon] = \mathbf{w} \mathbf{x}_1 + 0 = \mathbf{w} \mathbf{x}_1 \newline \operatorname{Var}(Y_1) &= \operatorname{Var}(\mathbf{w} \mathbf{x}_1) + \operatorname{Var}(\epsilon) = 0 + \sigma^2 = \sigma^2 \end{aligned}\]

进而我们可以得出 $Y_1 \vert \mathbf{x}_1 \sim \mathcal{N}(\mathbf{w} \mathbf{x}_1, \sigma^2)$，这就是我们在 $\mathbf{x}_1$ 处的 $\mathbb{P}_\text{model}$；然后所有 $\mathbf{x}_1$ 对应的 training data 构成 $\hat{\mathbb{P}}_\text{data}$，但在这里我们不需要知道 empirical distribution 具体长啥样，我们只关心 cross-entropy：

  • 你也可以把所有的 $Y_i$ 集合起来，这时 $\mathbb{P}_\text{model}$ 是一个多元的 Gaussian：$\mathbf{Y} \vert \mathbf{X} \sim \mathcal{N}(\mathbf{w} \mathbf{X}, \sigma^2)$
\[\begin{aligned} \mathbf{w}_{\text{ML}} &= \underset{\mathbf{w}}{\arg \max } \prod_{i=1}^{m} \mathbb{P}_{Y_i \vert \mathbf{x}_i} (y_i) \newline &= \underset{\mathbf{w}}{\arg \max } \sum_{i=1}^{m} \ln \mathbb{P}_{Y_i \vert \mathbf{x}_i} (y_i) \newline &= \underset{\mathbf{w}}{\arg \max } \sum_{i=1}^{m} \ln \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(y_i- \mathbf{w} \mathbf{x}_i)^{2}}{2 \sigma^{2}}} \newline &= \underset{\mathbf{w}}{\arg \max } -\frac{m}{2} \ln 2 \pi - \frac{m}{2} \ln \sigma^{2} - \frac{\sum_{i=1}^{m} (y_i- \mathbf{w} \mathbf{x}_i)^{2}}{2 \sigma^{2}} \newline &= \underset{\mathbf{w}}{\arg \min } \sum_{i=1}^{m} (y_i- \mathbf{w} \mathbf{x}_i)^{2} \newline &= \underset{\mathbf{w}}{\arg \min } \operatorname{MSE}(\mathbf{Y} \vert \mathbf{X}) \end{aligned}\]

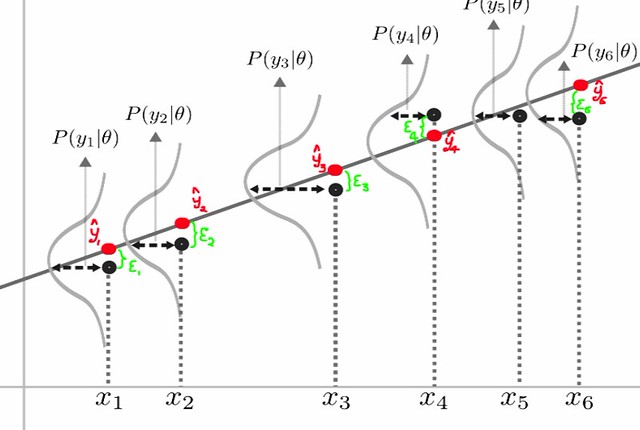
最后说一下 prediction：

  • 对一个新来的 test data point $\mathbf{x}_{m+1}$，prediction 很简单：$\hat{y}_{m+1} = \mathbf{w}_{\text{ML}} \mathbf{x}_{m+1}$。但这个式子是怎么得来的呢？
  • 因为我们的 assumption 是 $Y_{m+1} = \mathbf{w} \mathbf{x}_{m+1} + \epsilon$，所以我觉得应该把 prediction 理解成 $\hat{y}_{m+1} = \mathbb{E}[Y_{m+1}] = \mathbf{w}_{\text{ML}} \mathbf{x}_{m+1}$

6. Bayesian Generative Example: Naive Bayes Classifier

参考：

简单说就是 $\mathbf{D} = \mathbf{Y}, \mathbf{X}$，然后对任意一个 data point $(y^{(i)}, \mathbf{x}^{(i)})$，把 $\mathbf{x}^{(i)}$ 部分看成是一个 feature vector：$\mathbf{x}^{(i)} = \lbrace x^{(i)}_1,x^{(i)}_2,\cdots,x^{(i)}_n \rbrace$；然后 assume feature 之间是 independent 的，于是有：

\[\begin{aligned} \mathbb{P}(\mathbf{Y} \vert \mathbf{X}) &\propto \mathbb{P}(\mathbf{X} \vert \mathbf{Y}) \, \mathbb{P}(\mathbf{Y}) \newline &\propto \big( \prod_{i=1}^{n} \mathbb{P}(x_i \vert \mathbf{Y}) \big) \, \mathbb{P}(\mathbf{Y}) \end{aligned}\]

这个时候你把 $\mathbf{Y}$ 当做 $\theta$，$\mathbb{P}(\theta)$ 可以用 $\mathbf{Y}$ 的 empirical distribution 代替，于是有：

\[\begin{aligned} \mathbb{P}(\theta \vert \mathbf{X}) &\propto \big( \prod_{i=1}^{n} \mathbb{P}(x_i \vert \theta) \big) \, \mathbb{P}(\theta) \newline &\propto \sum_{i=1}^{n} \log \mathbb{P}(x_i \vert \theta) + \log \mathbb{P}(\theta) \end{aligned}\]

接着用 MAP 就可以了。

至于 $\mathbb{P}(x_i \vert \theta)$ 的 assumption 和处理，请看 Yao’s Blog: Naive Bayes classifier

Comments

You May Also Enjoy