Fisher’s Exact Test for Independence
总结自:
Fisher’s Exact Test is named after its inventor, Sir R. A. Fisher, and is one of a class of exact tests, so called because the significance of the deviation from a null hypothesis (e.g., p-value) can be calculated exactly, rather than relying on an approximation that becomes exact in the limit as the sample size grows to infinity, as with many statistical tests.
Fisher’s Exact Test 的 hypotheses 以及用途和 Chi-Square Test 完全一致,都是 to test whether two categorical variables are independent.
- $H_0$: variable $A$ and variable $B$ are independent.
- $H_a$: variable $A$ and variable $B$ are not independent.
两者的第一个区别在于:
- Chi-Square Test 对 sample size 是有要求的,不能太小
- Fisher’s Exact Test 在 sample size 小的时候仍然适用
第二个不同之处在于计算方法。Fisher’s Exact Test 不需要 test statistic,而是直接计算 probability 的(但是也不是直接计算 p-value),所以下面的重点在于计算方法。
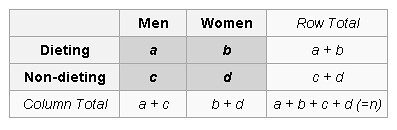
对如上图所示的任意的 2x2 table,the probability of obtaining any such set of values was given by the hypergeometric distribution:
\[p = \frac{ {a+b \choose a} {c+d \choose c} }{ {n \choose a+c} } = \frac{(a+b)! (c+d)! (a+c)!(b+d)!}{a!b!c!d!n!}\]- 因为 $a+c = n - (b+d)$,所以分母写 ${n \choose a+c}$ 或者 ${n \choose b+d}$ 是一样的。
To generate a significance level, we need consider only the cases where the marginal totals are the same as in the observed table, and among those, only the cases where the arrangement is as extreme as the observed arrangement, or more so. (Barnard’s test relaxes this constraint on one set of the marginal totals.)
换言之,对这样一个 table,
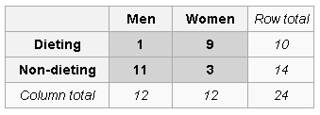
在 marginal totals 不变的情况下,我们要考虑其他的同样极端或者更极端的情况(更极端即意味着更小的 probability)。考虑到最小的 marginal total 是 10,所以 marginal totals 不变的情况下,这张表一共可能有 11 种(0~10 是 11 个数)变化形式,不计算概率,靠直觉我们也能得到一个更极端的形式是:
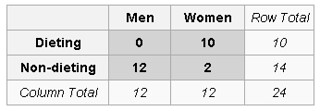
考虑分布的对称性,相反的反向应该也有两种情况,我们用矩阵来简单表示下:
- 已知的情况:$\begin{bmatrix}1 & 9 \newline 11 & 3 \end{bmatrix}$, 计算得 $p_1 = 0.001346076$
- 正方向更极端的情况:$\begin{bmatrix}0 & 10 \newline 12 & 2 \end{bmatrix}$, 计算得 $p_2 = 0.000033652$
- 反方向同样极端的情况:$\begin{bmatrix}9 & 1 \newline 3 & 11 \end{bmatrix}$, 计算得 $p_3 = p_1 = 0.001346076$
- 反方向更极端的情况:$\begin{bmatrix}10 & 0 \newline 2 & 12 \end{bmatrix}$, 计算得 $p_4 = p_2 =0.000033652$
- 如果我们只考虑正方向的两种情况,则我们做的是 one-tailed test,得到的 $\operatorname{p-value} = p_1 + p_2 = 0.001379728$ 也称为 one-tailed p-value 或者 1-sided p-value。
- 如果我们正反两个方向都考虑,则我们做的是 two-tailed test,得到的 $\operatorname{p-value} = p_1 + p_2 + p_3 + p_4 = 0.002759456$ 也称为 two-tailed p-value 或者 2-sided p-value。
- 一般情况下我们都应该做 two-tailed test,除非有客观的理由(比如反方向的情况是不存在的)
留下评论