Terminology Recap: Random Variable / Distribution / PMF / PDF / Independence / Marginal Distribution / Joint Distribution / Conditional Random Variable

主要参考：

• NOTES ON PROBABILITY - Greg Lawler
• Measure theory and probability - Alexander Grigoryan
• Lebesgue Measure on $\mathbb{R}^n$ - John K. Hunter
• Conditional random variables - Lawrence Pettit

Prerequisite #1 : $\sigma$-algebra

非常蛋疼的一个事实：$\sigma$-algebra 并不是一个严格意义上的 algebra……

Definition: In mathematical analysis and in probability theory, a $\sigma$-algebra on a set $S$ is a subset $\Sigma \subset 2^S$ that includes $S$ itself. It is closed under complement and countable unions.

• 因为 $S \in \Sigma$ 同时它是 closed under complement，所以 $\varnothing \in \Sigma$
• $\sigma$-algebra, $\sigma$-ring 和 $\sigma$-field 都是有关系的，但这里不表

Prerequisite #2 : Borel Set / Borel $\sigma$-algebra

In mathematics, a Borel set is any set in a topological space that can be formed from open sets (or, equivalently, from closed sets) through the operations of countable union, countable intersection, and relative complement.

• relative complement of $A$ in $B$ 就是 $A - B$
• relative complement of $B$ in $A$ 就是 $B - A$

For a topological space $X$, the collection of all Borel sets on $X$ forms a $\sigma$-algebra $\mathcal{B}$, known as the Borel algebra or Borel $\sigma$-algebra. The Borel $\sigma$-algebra on $X$ is the smallest $\sigma$-algebra containing all open sets (or, equivalently, all closed sets).

关于可数性：

• A set $S$ is said to be countable if it’s finite or $\mathbf{card}(S) = \mathbf{card}(\mathbb{N})$
• $\mathbf{card}(\mathbb{R}) > \mathbf{card}(\mathbb{N})$ (Cantor Diagonal Argument)
• If $\mathcal{B}$ is a Borel algebra in $\mathbb{R}$, then $\mathbf{card}(\mathcal{B}) = \mathbf{card}(\mathbb{R})$
  • 结论：$\mathcal{B}$ 不可数

Prerequisite #3 : Measurable Function / Measurable Space

Definition: A measurable space is a tuple of $(S, \Sigma)$ where $S$ is a set and $\Sigma$ is a $\sigma$-algebra over $S$.

• measurable space 又称 Borel space

Definition: Let $(X, \Sigma_X)$ and $(Y, \Sigma_Y)$ be measurable spaces. Function $f:X \to Y$ is called a measurable function if $\forall E_Y \in \Sigma_Y, f^{-1}(E_Y) \in \Sigma_X$

• $f^{-1}$ 是 inverse function
• 扩展一下 $f^{-1}$ 的定义：$f^{-1}(E_Y) := \lbrace x \in X \vert f(x) \in E_Y \rbrace$
• 这个定义相当于：$\forall E_Y \in \Sigma_Y, \exists E_X \in \Sigma_X$ 使得 $f(E_X) = E_Y$
  • 这个 $E_X$ 即 $f^{-1}(E_Y)$
• 为了强调 $f$ 是一个 measurable function，我们也可以把它写作 $f: (X, \Sigma_X) \to (Y, \Sigma_Y)$

Prerequisite #4 : Measure / Measure Space

Definition: Let $(S, \Sigma)$ be a measurable space. Function $\mu: \Sigma \to \mathbb{R} \cup \lbrace -\infty, \infty \rbrace$ is called a measure if it satisfies the following properties:

1. Non-negativity: $\forall E \in \Sigma, \mu(E) \geq 0$
   • 注：不满足这个条件的 measure 是存在的，比如 signed measure
2. Null empty set: $\mu(\varnothing) = 0$
3. Countable additivity (or $\sigma$-additivity): $\forall \text{ countable collection } \lbrace E_i \rbrace^{\infty}_{i=1}$ where $E_i \in \Sigma, \forall i$ and $E_i \cap E_j = \varnothing, \forall i, j$:

\[\mu \left( \bigcup _ { k = 1 } ^ { \infty } E _ { k } \right) = \sum _ { k = 1 } ^ { \infty } \mu \left( E _ { k } \right)\]

Definition: A measure space is such a triple of $(S, \Sigma, \mu)$

Prerequisite #5 : Probability Measure / Probability Space

Definition: Measure $\mu$ is probability measure if $\mu(S) = 1$.

• $S$ 指全集

Definition: A probability space is a measure space with a probability measure, denoted by $(\Omega, \mathcal{F}, \mathbb{P})$ where:

• $\omega \in \Omega$ is called an outcome
• $E \in \mathcal{F}$ is called an event
• $\mathbb{P}: \mathcal{F} \to [0,1]$ is a probability measure
  • $\mathbb{P}(E)$ is the probability of $E$

Prerequisite #3/#4/#5 Summary

• measurable function $f$ 定义在 measurable space $(S, \Sigma)$ 上
• measurable function $f$ 有潜力构成一个 measure $\mu$
• measure $\mu$ + measurable space $(S, \Sigma)$ = measure space $(S, \Sigma, \mu)$
  • probability measure $\mathbb{P}$ 是特殊的 measure
  • 装备 probability measure 的 measure space 是 probability space $(\Omega, \mathcal{F}, \mathbb{P})$

我们可以把 measurable function $f$ $\overset{\text{进化}}{\Rightarrow}$ measure $\mu$，但注意这里涉及一个定义域转化的问题：

• $f: S \to \mathbb{R}$
• $\mu: \Sigma \to \mathbb{R}$
• 比如我们可以定义 $\mu(\lbrace x \rbrace) = f(x)$ 然后根据 $\sigma$-additivity 有：

\[\mu(E) = \sum_{x \in E} \mu({\lbrace x \rbrace}) = \sum_{x \in E} f(x)\]

• 注意我这里的意思是：我们可以这样做，但没有规定说一定要这样做；$\mu$ 也不一定要通过 $f$ 定义，$f$ 也不一定满足进化成 $\mu$ 的要求

1. Random Variable

Definition: A random variable $X$ is a measurable function $X: (\Omega, \mathcal{F}) \to (\mathbb{R}, \mathcal{B})$ such that $\forall$ Borel set $B\in \mathcal{B}$

\[X^{-1}(B) \overset{\text{informal}}{=} \lbrace X \in B \rbrace = \lbrace \omega \in \Omega \vert X(\omega) \in B \rbrace \in \mathcal{F}\]

• 准确来说应该是 $\mathbb{R} \cup \lbrace -\infty, \infty \rbrace$ 而不仅仅是 $\mathbb{R}$
• $\mathcal{B}$ 是 $\mathbb{R}$ 上的 Borel $\sigma$-algebra

若 $X$ 是 $(\Omega, \mathcal{F}, \mathbb{P})$ 上的 random variable，那么：

• 我们称 $X$ 是 $\mathcal{F}$-measurable. We define $\mathcal{F}(X)$ to be the smallest $\sigma$-algebra on $\Omega$ for which $X$ is measurable.
• 比较一下 $X$ 和 $\mathbb{P}$:
  • 首先注意定义域：
    • $X: \Omega \to \mathbb{R}$ (random variable 接收 outcome)
    • $\mathbb{P}: \mathcal{F} \to [0, 1]$ (probability measure 接收 event)
  • $X$ 是 measurable function，$\mathbb{P}$ 是 probability measure，我们可以像上面 $f$ $\overset{\text{进化}}{\Rightarrow}$ $\mu$ 一样定义一个 $X$ 使它可以 $X$ $\overset{\text{进化}}{\Rightarrow}$ $\mathbb{P}$，但是！没有必要。后面 distribution 的部分会阐述。

以投骰子为例 (一个骰子，仅投一次)：

• $\Omega = \lbrace 1,2,3,4,5,6 \rbrace$
• $\mathcal{F}$ 包括但不限于 $\Omega$、$\lbrace 1 \rbrace$、$\lbrace 2 \rbrace$、$\lbrace 3 \rbrace$、$\lbrace 4 \rbrace$、$\lbrace 5 \rbrace$、$\lbrace 6 \rbrace$
• 假设有 $\mathbb{P}(\lbrace 1 \rbrace) = \mathbb{P}(\lbrace 2 \rbrace) = \mathbb{P}(\lbrace 3 \rbrace) = \mathbb{P}(\lbrace 4 \rbrace) = \mathbb{P}(\lbrace 5 \rbrace) = \mathbb{P}(\lbrace 6 \rbrace) = \frac{1}{6}$
  • 注意 event $\lbrace 1,3 \rbrace$ 表示 “roll 出 1 或者 3”，而不是 “roll 两次，一次是 1 一次是 3”
    • “roll 两次，一次是 1 一次是 3” 的 event 应该是 $\big \lbrace \lbrace 1,3 \rbrace \big \rbrace$
  • 所以 $\mathbb{P}(\lbrace 1,3 \rbrace) = \mathbb{P}(\lbrace 1 \rbrace) + \mathbb{P}(\lbrace 3 \rbrace) = \frac{1}{3}$，同理有 $\mathbb{P}(\Omega) = 1$
  • “roll 出 1 且 3” 是不可能事件，即 $\varnothing$，由 measure 的定义得到 $\mathbb{P}(\varnothing) = 0$

2. Distribution of a Random Variable

感谢 PhoemueX: On clarifying the relationship between distribution functions in measure theory and probability theory

假定有 probability space $(\Omega, \mathcal{F}, \mathbb{P})$，其上有一个 arbitrary 的 random variable $X$.

Definition: The push-forward measure of $\mathbb{P}$ by $X$ is a function $\mathbb{P}_{X}: \mathcal{B} \to \mathbb{R}$ such that $\forall B \in \mathcal{B}$,

\[\mathbb{P}_{X}(B) = \big (\mathbb{P} \circ X^{-1} \big )(B) = \mathbb{P}(X^{-1}(B)) \overset{\text{informal}}{=} \mathbb{P}(\lbrace X \in B \rbrace) = \mathbb{P}(\lbrace \omega \in \Omega \vert X(\omega) \in B \rbrace)\]

• 注意根据 random variable 的定义，$\forall B \in \mathcal{B}, X^{-1}(B) \in \mathcal{F}$，所以 $X^{-1}(B)$ 在 $\mathbb{P}$ 的定义域内
• $\mathbb{P}_{X}$ 一定是一个 probability measure，使得 $(\mathbb{R}, \mathcal{B}, \mathbb{P}_{X})$ 构成一个 probability space
• 若 $X = I$，即 $X(\omega) = \omega$，可得 $\mathbb{P}_{X} = \mathbb{P}$

我们称 $\mathbb{P}_{X}$ 为 distribution of random variable $X$.

我们这里重点考察一下 $\mathbb{P}_{X}$ 和 $\mathbb{P}$ 的关系，并引申出 $X$ 在其中的作用：

• $\mathbb{P}: \mathcal{F} \to [0, 1]$
• $X: (\Omega, \mathcal{F}) \to (\mathbb{R}, \mathcal{B})$
• 按理来说，$X^{-1}$ 应该是 $X^{-1}: \mathbb{R} \to \Omega$，但是我们通过 $X^{-1}(B)$ 的定义把它扩展成了 $X^{-1}: \mathcal{B} \to \mathcal{F}$
• 于是 $\mathbb{P}_{X} = \mathbb{P} \circ X^{-1}$ 就成了一个 $\mathcal{B} \to \mathcal{F} \to [0, 1]$ 的函数
• 所以 $X: \mathcal{F} \to \mathcal{B}$ 就可以看作一个 “event encoder“，它把每一个 event $E \in \mathcal{F}$ 映射到一个 Borel set $B \in \mathcal{B}$
• 同理$X^{-1}: \mathcal{B} \to \mathcal{F}$ 就可以看成一个 “event decoder“，它把每一个 Borel set $B \in \mathcal{B}$ 又映射回原来的 event $E \in \mathcal{F}$
• Event encoding 的作用在于：可以把各种不同的、具体的 $(\Omega, \mathcal{F})$ 转化为统一的、抽象的 $(\mathbb{R}, \mathcal{B})$
  • 比如 “投骰子” 和 “黑盒子里 6 个不同颜色的球，抓一个出来” 这两个实验，它们的 event 是不一样的，但我们明显可以看出它们的本质是一样的，这个本质体现在它们通过 $X$ encoding 以后，得到的 Borel set 是一样的 (或者说得到的 $\mathbb{P}_X$ 函数是一样的)
• Event decoding 的作用在于计算，因为 $\mathbb{P}_X$ 需要借助 $\mathbb{P}$ 才能算出具体的值
• 我们平时根本就没有注意到这个 event encoding/decoding 的过程是因为：它太顺理成章了。比如上面 “投骰子” 的例子，我们直接就写出了 $\Omega = \lbrace 1,2,3,4,5,6 \rbrace$，所以可以有 $E = B$，亦即 $X = I$，等于没有做 event encoding/decoding，于是我们也没有区分 $\mathbb{P}_{X}$ 和 $\mathbb{P}$，因为 $\mathbb{P}_{X} = \mathbb{P}$
• 但是我也可以定义说 $\Omega = \lbrace \text{I}, \text{II}, \text{III}, \text{IV}, \text{V}, \text{VI}\rbrace$，那你可能需要 encode 一下，得到:
  • $X(\text{I}) = 1$
  • $\dots$
  • $X(\text{VI}) = 6$
  • 所以 $\mathbb{P}_{X}(\lbrace 3 \rbrace) = \mathbb{P}(X^{-1}(\lbrace 3 \rbrace)) = \mathbb{P}(\lbrace \text{III} \rbrace)$
  • 当然，你的 $X$ 的定义可以不用与 event 的语义对应，比如我定义 $X(\text{I}) = 100, \dots, X(\text{VI}) = 600$，也是可以的

题外话：$\mathbb{P}(X = 3)$ 这种写法如何解释？

• 先说结论：这是个有点过分的简写
• 首先 $\mathbb{P}(X = 3)$ 应该是 $\mathbb{P}(\lbrace X = 3 \rbrace)$ ($\mathbb{P}$ 接收 event)
• 二来 $X = 3$ 应该理解为 $X \in \lbrace 3 \rbrace$
• 这么一来，令 $B = \lbrace 3 \rbrace$，套公式可得：

\[\mathbb{P}(X = 3) \overset{\text{informal}}{=} \mathbb{P}(\lbrace X = 3 \rbrace) \overset{\text{informal}}{=} \mathbb{P}(\lbrace X \in \lbrace 3 \rbrace \rbrace) = \mathbb{P}_X(\lbrace 3 \rbrace)\]

• 所以 $X = 3$ 整体是一个 event $E \in \mathcal{F}$ (informal)；而 $\lbrace 3 \rbrace$ 是一个 Borel set $B \in \mathcal{B}$
• 若 $X = I$，则 $E = B$, $\mathbb{P}_{X} = \mathbb{P}$，从而 $\mathbb{P}(X = 3) \overset{\text{informal}}{=} \mathbb{P}_X(\lbrace 3 \rbrace) = \mathbb{P}(\lbrace 3 \rbrace)$

$\mathbb{P}_{X}$ 的性质还有：

• If $\mathbb{P}_{X}$ gives measure one to a countable set of reals, then $X$ is called a discrete random variable.
  • $\mathbb{P}_{X}: \mathcal{B} \to [0, 1]$, 然后 $\mathcal{B}$ 不可数
  • 但 $\mathbb{P}_{X}$ 的 domain 可能只是 $\mathcal{B}$ 的一个可数子集
• If $\mathbb{P}_{X}$ gives zero measure to every singleton set, and hence to every countable set, $X$ is called a continuous random variable.
  • Every random variable can be written as a sum of a discrete random variable and a continuous random variable.
  • All random variables defined on a discrete probability space are discrete

Definition: 对任意的 (locally finite) measure $\mu$ on $\mathbb{R}$，我们定义 distribution function of $\mu$ as

\[F_{\mu}(x) = \mu \big ( (-\infty, x] \big)\]

那既然 $\mathbb{P}_{X}$ 是一个 probability measure (probability measure 一定是 locally finite)，我们可以定义：

\[F_{\mathbb{P}_{X}}(a) = \mathbb{P}_{X} \big ( (-\infty, a] \big) = \mathbb{P} \Big ( X^{-1}\big ( (-\infty, a] \big) \Big) \overset{\text{informal}}{=} \mathbb{P}\big ( \lbrace X \in (-\infty, a] \rbrace \big ) \overset{\text{informal}}{=} \mathbb{P}(X \leq a)\]

严格来说，$F_{\mathbb{P}_{X}}$ 应该叫做 distribution function of the distribution of random variable $X$，但是非常不幸的是，它也被简称为 distribution of random variable $X$，并且简化符号为 $F_X = F_{\mathbb{P}_{X}}$

3. Probability Mass Functions (for the discrete), and Probability Density Functions (for the continuous)

Definition: Probability mass function for discrete random variable $X$, $p_X: \mathbb{R} \to [0, 1]$, can be defined as:

\[\begin{aligned} p_X(x) &= \mathbb{P}(X = x) = \mathbb{P}_X(\lbrace x \rbrace) \newline \sum_{x \in \mathbb{R}} p_X(x) &= 1 \end{aligned}\]

其实就是把 $\mathbb{P}_X$ 的定义域中的 one-element $B \in \mathcal{B}$ 的部分降维到了 $x \in \mathbb{R}$，就是这么简单。

Definition: Probability density function for continuous random variable $X$, $f_X: \mathbb{R} \to [0, \infty)$, is one satisfying:

\[\begin{aligned} \int_{a}^{b} f_X(x) \mathrm{d}x &= \mathbb{P} \big ( \lbrace a \leq X \leq b \rbrace \big ) = F_X(b) - F_X(a) \newline \int_{-\infty}^{\infty} f_X(x) \mathrm{d}x &= 1 \end{aligned}\]

• 严格来说，$f_X$ 应该叫做 “the density or Radon–Nikodym derivative with respect to Lebesgue measure of random variable $X$”

若 $f_X$ 存在：

• 我们可以写 $F_X(x) = \int_{-\infty}^{x} f_X(t) \mathrm{d}t$
• If $f_X$ is continuous at $t \Rightarrow f_X(x) = F_X’(x)$

4. Tilde $\sim$ / i.i.d.

根据 Ben O’Neill: Why are probability distributions denoted with a tilde?，$\sim$ 其实是一个 equivalence relation，所以 $X \sim Y$ 左右两边都是 random variable，它可以念做 “$X$ has the same distribution as $Y$”。我觉得这基本就是 $X = Y$ 的意思了。

• 所以 $\mathcal{N}(0, 1)$ 它不是 distribution，而是一个 random variable
• 如果 $X \sim \mathcal{N}(0, 1)$，那么 $X(x) = \mathcal{N}(x; 0, 1)$
• 如果 $\mu, \sigma^2$ 不确定，$\mathcal{N}(\mu, \sigma^2)$ 可以看做一个 parametric random variable
  • 注意如果有 $X \sim \mathcal{N}(\mu, \sigma^2)$，那么这里 $\mathcal{N}(\mu, \sigma^2)$ 一定是表示一个具体的 random variable (once $\mu, \sigma^2$ 确定下来)，而不能理解为是一个 family of random variables

那么问题来了：”has the same distribution as” 这个 distribution 指的是 $\mathbb{P}_{X}$ 还是 $F_X = F_{\mathbb{P}_{X}}$？

• 若 $X \sim Y$ 都是 discrete random variable，那么明显 $\mathbb{P}_{X}$ 更直接，所以一般我们用 $\mathbb{P}_{X} = \mathbb{P}_{Y}$ 这个结论
  • 进而有 $p_X = p_Y$
• 若 $X \sim Y$ 都是 continuous random variable，那么明显 $F_X$ 才有意义，所以一般我们用 $F_X = F_Y$ 这个结论
  • 进而有 $f_X = f_Y$

我们直接研究 random variable $X$ 即意味着我们跳过了 event encoding/decoding 的步骤，直接在 $(\mathbb{R}, \mathcal{B}, \mathbb{P}_{X})$ 这个抽象的 probability space 上工作，至于原来的 $(\Omega, \mathcal{F}, \mathbb{P})$ 长什么样子我们就不关心了。

另外还有一个常见的概念是 i.i.d. (independent and identically distributed)，它是用来形容一组 random variables 的。简单说，如果 $X_1, \dots , X_n$ 是一组 i.i.d. 的 random variables，那么：

• $X_1 \sim X_2 \sim \dots X_{n-1} \sim X_n$ (我觉得诡异的是这么多年我就没见过哪本教材用这个式子来描述 i.i.d.)
• $X_1, \dots , X_n$ 互相是 independent 的

5. Independence / Marginal Distribution / Join Distribution

我们先从 $(\Omega, \mathcal{F}, \mathbb{P})$ 的层次入手。

Definition: (1) Two events $E_1, E_2$ are called independent if

\[\mathbb{P}(E_1 \cap E_2) = \mathbb{P}(E_1) \mathbb{P}(E_2)\]

(2) A collection of events $\lbrace E_i \rbrace$ is called independent if $\forall$ distinct $E_1, \dots, E_n$,

\[\mathbb{P}(E_1 \cap \dots \cap E_n) = \mathbb{P}(E_1) \dots \mathbb{P}(E_n)\]

(3) A collection of events $\lbrace E_i \rbrace$ is called pairwise independent if $\forall$ distinct $E_i, E_j$,

\[\mathbb{P}(E_i \cap E_j) = \mathbb{P}(E_i) \mathbb{P}(E_j)\]

(4) A finite collection of $\sigma$-algebras $\mathcal{F}_1, \dots, \mathcal{F}_n$ is called independent if $\forall$ $E_1 \in \mathcal{F}_1, \dots, E_n \in \mathcal{F}_n$, $\lbrace E_1, \dots, E_n \rbrace$ is independent.

(5) An infinite collection of $\sigma$-algebras is called independent if every subcollection is independent.

If $X_1, \dots , X_n$ are random variables, we can consider them as a random vector $(X_1, \dots , X_n)$ and hence as ONE random variable $X_{1:n}: \mathcal{B(\mathbb{R}^n)} \to \mathbb{R}^n$

• Let $\mathcal{T}(\mathbb{R}^n) \subset \mathcal{P}(\mathbb{R}^n)$ denote the standard topology on $\mathbb{R}^n$ consisting of all open sets
  • $\mathcal{P}(S) = 2^S$
• $\mathcal{B(\mathbb{R}^n)}$ is the $\sigma$-algebra generated by all the open set, i.e. $\mathcal{B(\mathbb{R}^n)} = \sigma \big ( \mathcal{T}(\mathbb{R}^n) \big )$

假设原有 probability spaces $(\Omega_1, \mathcal{F}_1, \mathbb{P}_1), \dots, (\Omega_n, \mathcal{F}_n, \mathbb{P}_n)$，令 $\Omega_{1:n} = \Omega_1 \times \dots \times \Omega_n$, $\mathcal{F}_{1:n} = \mathcal{F}_1 \otimes \dots \otimes \mathcal{F}_n$, $\mathbb{P}_{1:n} = \mathbb{P}_1 \times \dots \times \mathbb{P}_n$. 注意，根据 Wikipedia: Product measure：

• $\Omega_1 \times \Omega_2$ is the Cartesian product of the two sets
• $\mathcal{F}_1 \otimes \mathcal{F}_2$ is the $\sigma$-algebra on $\Omega_1 \times \Omega_2$, generated by subsets of the form $E_{1} \times E_{2}$ where $E_{1} \in \mathcal{F}_{1}$ and $E_{2} \in \mathcal{F}_{2}$
• A product measure $\mathbb{P}_1 \times \mathbb{P}_2$ is defined to be a measure on the measurable space $(\Omega_1 \times \Omega_2, \mathcal{F}_1 \otimes \mathcal{F}_2)$ satisfying $\forall E_{1} \in \mathcal{F}_{1}, \forall E_{2} \in \mathcal{F}_{2}$,

\[(\mathbb{P}_1 \times \mathbb{P}_2)(E_{1} \times E_{2}) = \mathbb{P}_1(E_1) \mathbb{P}_2(E_2)\]

假设 $X_1$ 是 $(\Omega_1, \mathcal{F}_1, \mathbb{P}_1)$ 上的 random variable，$\dots$，$X_n$ 是 $(\Omega_n, \mathcal{F}_n, \mathbb{P}_n)$ 上的 random variable。然后我们有一批：

• distribution: $\mathbb{P}_{X_1}, \dots, \mathbb{P}_{X_n}$
• distribution function of distribution: $F_{X_1}, \dots, F_{X_n}$
• PMF: $p_{X_1}, \dots, p_{X_n}$
• PDF: $f_{X_1}, \dots, f_{X_n}$

Definition: For random variable $X_{1:n} = (X_1, \dots , X_n)$, its joint distribution $\mathbb{P}_{X_{1:n}}: \mathcal{B(\mathbb{R}^n)} \to \mathbb{R}$ can be defined as: $\forall B_{1:n} = B_1 \times \dots \times B_n$, $B_{1:n} \in \mathcal{B(\mathbb{R}^n)}$

\[\mathbb{P}_{X_{1:n}}(B_{1:n}) = \mathbb{P}_{1:n} \big (X_{1:n}^{-1}(B_{1:n}) \big) \overset{\text{informal}}{=} \mathbb{P}_{1:n} \big ( \lbrace X_{1:n} \in B_{1:n} \rbrace \big ) \overset{\text{informal}}{=} \mathbb{P}_{1:n} \big ( \lbrace X_1 \in B_1, \dots, X_n \in B_n \rbrace \big )\]

Definition: For joint distribution $\mathbb{P}_{X_{1:n}}$, its joint distrbution function $F_{X_{1:n}} \overset{\text{abbrev.}}{=} F_{\mathbb{P}_{X_{1:n}}}: \mathbb{R}^n \to [0, 1]$ can be defined as: $\forall t_i \in \mathbb{R}$

\[F_{X_{1:n}}(t_1, \dots, t_n) \overset{\text{informal}}{=} \mathbb{P}_{1:n} \big ( \lbrace X_1 \leq t_1, \dots, X_n \leq t_n \rbrace \big ) = \mathbb{P}_{X_{1:n}} \big ( (-\infty, t_1] \times \dots \times (-\infty, t_n] \big )\]

Definition: For random variable $X_{1:n} = (X_1, \dots , X_n)$, its joint probability mass function $p_{X_{1:n}}: \mathbb{R}^n \to [0, 1]$ can be defined as:

\[\begin{aligned} p_{X_{1:n}}(x_1, \dots, x_n) &= \mathbb{P}_{X_{1:n}} \Big ( \big \lbrace \lbrace x_1, \dots, x_n \rbrace \big \rbrace \Big ) = \mathbb{P}_{1:n}(\lbrace x_1, \dots, x_n \rbrace) \newline \sum_{\vec x \in \mathbb{R}^n} p_{X_{1:n}}(\vec x) &= 1 \end{aligned}\]

Definition: For random variable $X_{1:n} = (X_1, \dots , X_n)$, its joint probability density function $f_{X_{1:n}}: \mathbb{R}^n \to [0, \infty]$ is one statisfying: $\forall B_{1:n} = B_1 \times \dots \times B_n, B_{1:n} \in \mathcal{B(\mathbb{R}^n)}$,

\[\begin{aligned} \int_{B_{1:n}} f_{X_{1:n}}(x_1, \dots, x_n) \mathrm{d}x_1 \dots \mathrm{d}x_n &= \mathbb{P}_{X_{1:n}}(B_{1:n}) \newline \int_{\mathcal{B(\mathbb{R}^n)}} f_{X_{1:n}}(x_1, \dots, x_n) \mathrm{d}x_1 \dots \mathrm{d}x_n &= 1 \end{aligned}\]

Definition: Random variables $X_1, \dots, X_n$ are said to be independent if any of these (equivalent) conditions hold:

(1) Joint distribution is the product of all marginal distributions:

\[\begin{aligned} \mathbb{P}_{X_{1:n}}(B_{1:n}) \overset{\text{informal}}{=} & \mathbb{P}_{1:n} \big ( \lbrace X_1 \in B_1, \dots, X_n \in B_n \rbrace \big ) \newline = &\mathbb{P}_{1}(\lbrace X_1 \in B_1 \rbrace) \dots \mathbb{P}_{n}(\lbrace X_n \in B_n \rbrace) \newline = &\mathbb{P}_{X_1}(B_1) \dots \mathbb{P}_{X_n}(B_n) \end{aligned}\]

• This is equivalent of saying “joint distribution is the product measure of all marginal distributions”:

\[\mathbb{P}_{X_{1:n}} = \mathbb{P}_{X_1} \times \dots \times \mathbb{P}_{X_n}\]

• Marginal distribution of $X$ 其实就是 $X$’s individual distribution，它只在 joint distribution 这个 context 下有意义。语出二维的 discrete joint distribution table，比如：

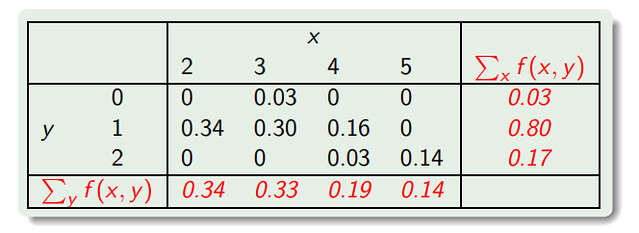
(2) Joint distribution function is the product of all marginal distribution functions:

\[\begin{aligned} F_{X_{1:n}}(t_1, \dots, t_n) &= \mathbb{P}_{X_{1:n}} \big ( (-\infty, t_1] \times \dots \times (-\infty, t_n] \big ) \newline &= \mathbb{P}_{X_1} \big ( (-\infty, t_1] \big ) \dots \mathbb{P}_{X_n} \big ( (-\infty, t_n] \big ) \newline &= F_{X_1}(t_1) \dots F_{X_n}(t_n) \end{aligned}\]

(3) Joint PMF is the product of all individual PMFs:

\[\begin{aligned} p_{X_{1:n}}(x_1, \dots, x_n) &= \mathbb{P}_{X_{1:n}} \Big ( \big \lbrace \lbrace x_1, \dots, x_n \rbrace \big \rbrace \Big ) \newline &= \mathbb{P}_{X_1} \big ( \lbrace x_1 \rbrace \big ) \dots \mathbb{P}_{X_n} \big ( \lbrace x_n \rbrace \big ) \newline &= p_{X_1}(x_1) \dots p_{X_n}(x_n) \end{aligned}\]

(4) Joint PDF (if exists) is the product of all individual PDFs:

\[f_{X_{1:n}}(x_1, \dots, x_n) = f_{X_1}(x_1) \dots f_{X_n}(x_n)\]

(5) The $\sigma$-algebras $\mathcal{F}(X_1), \dots \mathcal{F}(X_n)$ are independent.

6. Conditional Random Variable

Suppse $X, Y$ are discrete random variables over $(\Omega, \mathcal{F}, \mathbb{P})$. If $\mathbb{P}(Y = y) \neq 0$, then we can define the conditional probability (measure):

\[\mathbb{P}(X = x \mid Y = y) = \frac{\mathbb{P}(X = x \text{ and } Y = y)}{\mathbb{P}(Y = y)}\]

Definition: The discrete conditional random variable $X \mid Y = y$, read “$X$ given $Y = y$”, has PMF

\[p_{X \mid Y = y}(x) = \mathbb{P} \big ( (X \mid Y = y) = x \big ) = \mathbb{P}(X = x \mid Y = y)\]

Similarly, we can have

Definition: The continuous conditional random variable $X \mid Y = y$, has PDF

\[f_{X \mid Y = y}(x) = \frac{f_{X, Y}(x, y)}{f_Y(y)}\]