Python: Heaps

参考:

• Binary Heaps
• 7.10. Binary Heap Implementation
• How can building a heap be O(n) time complexity?

1. Heaps

1.1 Definition

heap 从结构上来说是一个 complete binary tree，数据上它要满足 heap ordering property，分两种：

• min-heap: $\forall$ node v, v.data >= v.parent.data
  • root.data 是最小值
• max-heap: $\forall$ node v, v.data <= v.parent.data
  • root.data 是最大值
• 注意我们并没有规定 sibling 之间的大小关系

下图左边是 min-heap，右图是 max-heap：

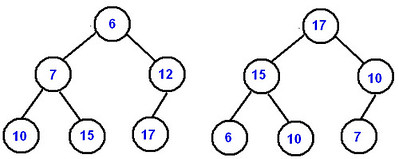
1.2 Array Implementation of Heaps / Index 换算

complete binary tree 有一个特点：它可以 uniquely 被它的 level-order traversal 表示。换言之，我们可以用一个 list N 来表示一个 complete binary tree，N 中的节点满足下列关系：

N[i].left is N[2 * i + 1]  # 定位 left child (when i < len(N) // 2)
N[i].right is N[2 * i + 2]  # 定位 right child (when i < len(N) // 2)

N[i].parent is N[(i-1) // 2]  # 定位 parent (when i >= 1)

N[: len(N) // 2]  # 全部都是 non-leaves
N[len(N) // 2 :]  # 全部都是 leaves

那由于 heap 本质是一个 complete binary tree，所以 heap 也可以用一个 array 表示，比如上图的 min-heap 可以表示为：

[6, 7, 12, 10, 15, 17]

在具体实现的时候，为了方便计算下标，有的 lib 的 heap 是不用 N[0] 的，直接从 N[1] 开始，此时有：

N[i].left is N[2 * i]  # 定位 left child (when i <= len(N) // 2)
N[i].right is N[2 * i + 1]  # 定位 right child (when i <= len(N) // 2)

N[i].parent is N[i // 2]  # 定位 parent (when i >= 2)

N[1: len(N) // 2 + 1]  # 全部都是 non-leaves
N[len(N) // 2 + 1 :]  # 全部都是 leaves

1.3 Internal Heap Operations

heap 有两个核心的内部操作：

• sift_down (也有地方叫做 percolate_down)
• sift_up (也有地方叫做 percolate_up)

从翻译的角度来讲：

• sift 指类似 “用筛子筛面粉” 的 “筛” 这个动作
• percolate 指类似 brewing coffee 那样的 “液体的渗漏、渗出” (或者类似塞尔达的下载地图？)

那以下都以 min-heap 为例。简单来说：

• sift_down(i) 是把一个大元素 (当前位于 N[i]) 逐渐移动到 heap 低层的操作 (往 leaves 方向下行)
• sift_up(i) 是把一个小元素 (当前位于 N[i]) 逐渐移动到 heap 高层的操作 (往 root 方向上行) (bubble up 的感觉？)

1.3.1 Insert A New Node & sift_up

insert 一个新元素到 min-heap 可以这么做：

1. 先不管三七二十一直接把新元素 append 到 heap array 尾部
2. 根据新元素的 index 找它的 parent 的 index，比较大小。如果新元素小于它的 parent，swap
3. 依此类推，一路往上 swap

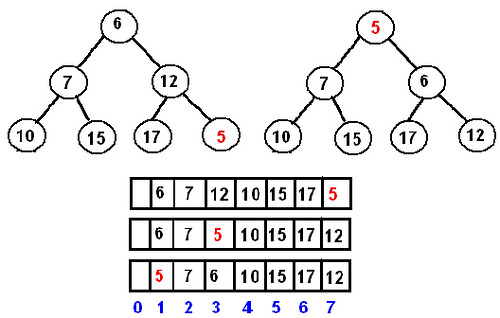
这个 “把元素往上层 swap” 的操作即是 sift_up，它的 time complexity：

• worst-case: $O(\log n)$
• worst-case 就是每一层都 swap 了一次，一直 swap 到 root

1.3.2 Delete The Root & sift_down

还是用 min-heap 举例。delete 掉 root 也就是 delete 掉 minimun，可以这么做：

1. 不管三七二十一直接用 heap array 的最后一个 node 来 overwrite root (然后把这最后一个 node 从 heap array 尾部删除)
2. 类似 insert 的逻辑，只是此时你要找这个新 root 的 children 做比较。稍微与 sift_up 不同的是，此时你要比较三个元素，你的目的是把 min(root, root.left, root.right) swap 到 root 的位置
3. 依此类推，一路往下 swap

这个 “把元素往下层 swap” 的操作我们称为 sift_down，它的 time complexity：

• worst-case: $O(\log n)$
• 注意 worst-case 到不了 $O(n)$，因为你每一层都至多比较两次，不会和所有的 node 都比较一次

1.3.3 Build A Heap From A List (heapify)

其实从下列两个方向构建都是可行的，但是在 performance 上有区别。

1.3.3.1 Top-down with sift_up

大致等价于下面的代码：

def heapify(lst):
    heap = lst

    for i in range(len(heap)):
        heap.sift_up(i)

    return heap

要注意这么几点：

• sift_up 并不是和 “insert 新节点” 操作绑定的，你不做 insert 操作也可以调用 sift_up
  • 或者你这么理解：这个用 sift_up 的 heapify 的操作就相当于是 lst 的元素一个接一个地 insert 到一个初始为空的 heap 中
• 我们做 sift_up 的时候是要假设 “旧的 heap 是合法的”。在我们这个循环 sift_up 的过程中，sift_up(i) 时我们只 care i 之前的元素，which 在 sift_up(i-1) 时已近是在一个合法的 heap 结构里了，所以这个假设一直是满足的
  • 换言之，我们在 sift_up(i) 时，i 之后的元素是不是满足 heap 结构我们不 care

1.3.3.2 Bottom-up with sift_down

从低层构造的话，有这么几个 insights：

• leaf 节点不需要做 sift_down
• 必须要等到低层节点的 sift_down 做完了，高层节点才能做 sift_down
  • 因为 sift_down 要 assume 底下的 subtree 是满足 heap ordering property，所以低层的 percolate down 要先做

所以这个过程大致等价于下面的代码 (假定使用 N[0])：

def heapify(lst):
    heap = lst

    non_leaf_indices = range(0, len(heap) // 2)

    for i in reversed(non_leaf_indices):
        heap.sift_down(i)

    return heap

举例：比如这个 [9, 6, 5, 2, 3]，做了两次 sift_down，注意第二次 i=1 时 (不使用 N[0] 所以 N[1] 是 root) 时，是 swap 了两次

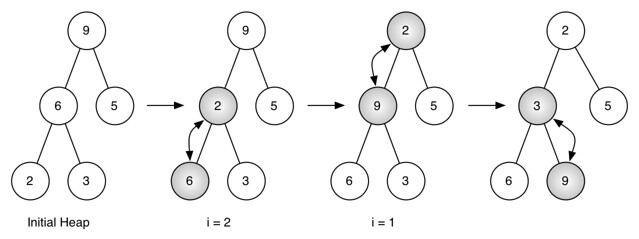
1.3.3.3 Performance Analysis

How can building a heap be O(n) time complexity? 答案里有很精彩的分析。

以下我们考虑 worst case，假设每次 comparison 都执行了 swap。

Top-down with sift_up:

• root，1 个元素，每个 swap 0 次
• 第二层，2 个元素，每个 swap 1 次
• 第三层，4 个元素，每个 swap 2 次
• …
• 第 h 层，$\frac{n}{2}$ 个元素 (leaves)，每个 swap $h-1$ 次

总共要 swap 这么多次：

\[\frac{n}{2} \times (h-1) + \frac{n}{4} \times (h-2) + \dots + 2 \times 1 + 1 \times 0\]

然后有 $h = \log n$。考虑到最后一层已经是 $O(n \log n)$ 了，所以 Top-down with sift_up 的 worst-case time complexity 是 $O(n \log n)$。

Bottom-up with sift_down：

• 第 h 层，$\frac{n}{2}$ 个元素 (leaves)，每个 swap 0 次
• 第 h-1 层，$\frac{n}{4}$ 个元素，每个 swap $1$ 次
• …
• 第三层，4 个元素，每个 swap $h-3$ 次
• 第二层，2 个元素，每个 swap $h-2$ 次
• root，1 个元素，每个 swap $h-1$ 次

总共要 swap 这么多次：

\[\frac{n}{2} \times 0 + \frac{n}{4} \times 1 + \dots + 2 \times (h-2) + 1 \times (h-1)\]

这个和式按 Taylor series 展开可以得到极限 $n$，所以 Bottom-up with sift_down 的 worst-case time complexity 是 $O(n)$。

1.4 Vanilla Heap Implementation

下面我们来手动写一个不使用 N[0] 的 min-heap

• 额外加了一个 current_size 字段，避免总是去取 len(N)

class MinHeap:
    def __init__(self):
        self.heap_list = [None]  # slot [0] 不使用，直接赋值为 None
        self.current_size = 0
    
    def sift_up(self, index):
        while index // 2:
            parent_index = index // 2
            
            if self.heap_list[parent_index] > self.heap_list[index]:
                self.heap_list[parent_index], self.heap_list[index] = self.heap_list[index], self.heap_list[parent_index]
                index = parent_index
            else:
                break
                
    def _get_min_child_index(self, index):
            left_child_index = index * 2
            right_child_index = index * 2 + 1
            
            if left_child_index > self.current_size:  # 说明 index 是个 leaf，它不应该做 sift_down
                raise ValueError("index points to a leaf node; cannot percolate down")
            elif right_child_index > self.current_size:  # 说明 index 只有 left child，没有 right child
                return left_child_index
            else:  # 儿女双全，需要比较一下
                return left_child_index if self.heap_list[left_child_index] <= self.heap_list[right_child_index] else right_child_index
    
    def sift_down(self, index):
        while index * 2 <= self.current_size:  # 当 index 还没哟有到 leaf 层时
            mc_index = self._get_min_child_index(index)
            
            if self.heap_list[mc_index] < self.heap_list[index]:
                self.heap_list[mc_index], self.heap_list[index] = self.heap_list[index], self.heap_list[mc_index]
                index = mc_index
            else:
                break
                
    def insert(self, element):
        self.heap_list.append(element)
        self.current_size += 1
        
        last_index = self.current_size
        self.sift_up(last_index)
        
    def pop_minimum(self):
        root = self.heap_list[1]  # retrieve the root value; need to return this in the end
        
        self.heap_list[1] = self.heap_list[self.current_size]  # 把队尾放到 root 的位置
        self.heap_list.pop()  # 删除掉原来的队尾
        self.current_size -= 1
        
        self.sift_down(1)
        
        return root
    
    def get_minimum(self):
        return self.heap_list[1]
    
    def heapify(self, elements):
        self.heap_list = [None] + elements
        self.current_size = len(elements)
        
        non_leaf_indices = reversed(range(1, self.current_size // 2 + 1))
        for index in non_leaf_indices:
            self.sift_down(index)
            
    def __str__(self):
        return str(self.heap_list[1:])
    
    def __len__(self):
        return self.current_size

heap = MinHeap()
heap.heapify([6, 7, 10, 12, 15, 17])

"""
     6
   /   \
  7     10
 / \   /
12 15 17
"""

print(heap)
# Output: [6, 7, 10, 12, 15, 17]

heap.insert(5)

"""
     5
   /   \
  7     6
 / \   / \
12 15 17  10
"""

print(heap)
# Output: [5, 7, 6, 12, 15, 17, 10]

print(heap.pop_minimum())
# Output: 5

"""
     6
   /   \
  7     10
 / \   /
12 15 17
"""

print(heap)
# Output: [6, 7, 10, 12, 15, 17]

另外在帖子 Implementing heap in Python 提到了：可以使用 generic 的 less-than operator 来比较 element 的大小，进而实现 object 的 heap (类似于 java 的 Comparator 接口的思想)

import operator

def __init__(self, heap=None, comparator=operator.lt):
    self.heap_list = [None]  # slot [0] 不使用，直接赋值为 None
    self.current_size = 0
    self.comparator = comparator

这个帖子里的 heapify 函数其实是我们 sift 的意思，不用深究。我们的叫法是对的。

2. Heap Sort

之前说 heap sort 都觉得特别高大上，其实现在看来很简单：

1. 上来 heapify => $O(n)$
2. 持续 pop 掉 root，做 $n$ 次 => $O(n \log n)$
   • 最后总的 time complexity 还是 $O(n \log n)$

因为每次 pop 出来的都是当前的 minimum，所以排列出来就是个 ascending 的顺序。

def heap_sort(elements):
    heap = MinHeap()
    heap.heapify(elements)
    
    def generate_minimums(heap):
        while heap:
            yield heap.pop_minimum()
            
    return list(generate_minimums(heap))

heap_sort([1, 3, 4, 6, 2, 5])
# Output: [1, 2, 3, 4, 5, 6]

这个 time complexity 其实可以深究一下，因为在你不断 pop 的过程中，tree 在 shrinking，层数会逐渐降低，似乎不是简单的每个节点都是 $O(\log n)$。但仔细分析下有：

• 第 h 层，$\frac{n}{2}$ 个元素 (leaves)，每个都要做 $O(h-1)$ 的 sift_down
• 第 h-1 层，$\frac{n}{4}$ 个元素，每个都要做 $O(h-2)$ 的 sift_down
• …
• 第三层，4 个元素，每个都要做 $O(2)$ 的 sift_down
• 第二层，2 个元素，每个都要做 $O(1)$ 的 sift_down
• root，1 个元素，不用做 sift_down

所以它的情况和 Top-down heapify with sift_up 的情况很像：

\[\frac{n}{2} \times (h-1) + \frac{n}{4} \times (h-2) + \dots + 2 \times 1 + 1 \times 0\]

最终还是 $O(n \log n)$

3. Python heapq Module

3.1 Basic Operations

注意：

• python 是 implicitly 提供了 heap 的数据结构，我这么说是因为 heapq 完全是个 util module，所以一般你是 heapq.xxx(heap) 而不是 heap.xxx()
• heapq 隐藏了 sift_down 和 sift_up (但还是能强行 import 出来)

基本操作有：

from heapq import heapify, heappop, heappush, heapreplace, heappushpop

h = [3, 2, 1] 
heapify(h)  # 注意这是个 in-place 操作，将 list 直接转成 heap

root = heappop(h)  # 相当于上面的 self.pop_minimum()

heappush(h, e)  # in-place 操作，相当于上面的 self.insert(e)

# 容易混淆的两个操作，这个 heapreplace 的命名我没有看懂
root = heapreplace(h, e)  # 先 root = heappop(h)，然后 heappush(h, e)
root = heappushpop(h, e)  # 先 heappush(h, e)，然后 root = heappop(h)

3.2 nlargest / nsmallest / $k$ 路归并

那除了对 heap 本身的操作之外，heapq 还要三个 heap sort 相关的函数：

from heapq import nlargest, nsmallest, merge

"""
这个 key 是一个 key function:

- 它可以是一个 field accessor，比如 key = lambda obj: obj.attribute
    - 然后元素就按它们的这个字段的大小来排序
- 也可以有其他的用法，比如 key = abs
- 总之，它的意思就是：在比较元素大小时，使用 key(e) 的值来比较
- 如果 key is None，说明是直接比较元素本身
"""
nlargest(n, iterable, key=None)  # 返回 iterable 中最大的 n 个元素，返回值的数据结构是 list
nsmallest(n, iterable, key=None)  # 返回 iterable 中最小的 n 个元素，返回值的数据结构是 list

# heapq.merge 即是传说中的 k 路归并算法！ (k-way merging)
    # *iterables 是 k 个 iterable，而且要求它们自身是 sorted 的
    # k-way merging 就是把这个 k 个 iterable 合并排序
merge(*iterables, key=None, reverse=False)

$k$ 路归并可以参考 Python: Vanilla k-way Merge Implementation & Lexical Order

4. Priority Queue

priority queue 是一个 abstract data structure，类似 interface 的意思，只要求了功能，没有要求具体实现。

• 功能上，带 priority 的 tasks 会被丢进 priority queue，然后总是 high priority 的 task 被先执行。
• 实现上，可以用 array、linked list 和 heap
  • array 的实现又分两种：
    1. 每次 push 的时候直接 append，等到要 pop 的时候再做 sorting (先甜后苦)
    2. 每次 push 的时候就直接做 sorting，pop 的时候就直接 pop (先苦后甜)
  • linked list 和 array 的实现差不多
  • heap 还是比 array、linked list 要快一点的

	insert	deleteMin	findMin
ordered array	O(n)	O(1)	O(1)
ordered list	O(n)	O(1)	O(1)
unordered array	O(1)	O(n)	O(n)
unordered list	O(1)	O(n)	O(n)
binary heap	O(log n)	O(log n)	O(1)