LR Parsing #8: LALR(1) as Approximation of LR(1)

Reference:

• Stanford CS143 Handout 14 - LALR Parsing
• Parsing Techniques, 2nd Edition

1. Intuition & Example

$LR(1)$ 有一个很明显的问题就是 item/state space 的爆炸式增长；$LALR(1)$ 的想法是 “to merge $LR(1)$ states with the same core by combining their lookaheads, thus lowering the total count of states”.

这里需要正式定义一下 core:

Definition: The core of an $LR(1)$ state is its $LR(0)$ items (i.e. the item set with their lookaheads dropped). $\blacksquare$

注意与 kernel item 区分。

所以如果两个 $LR(1)$ states 的 core 相同，$LALR(1)$ 认为它们就可以合并，合并的方式是把相同 item 的 lookaheads 取 union.

举个例子：

S' -> S
S -> XX
X -> aX
X -> b

---
config:
  layout: elk
  look: handDrawn
---
flowchart LR
    subgraph I0["State#0"]
        direction TB
        i00["$$S' \to \cdot S, \Finv$$"] ~~~
        i01["$$S \to \cdot XX, \Finv$$"] ~~~
        i02["$$X \to \cdot aX, \lbrace a, b \rbrace$$"] ~~~
        i03["$$X \to \cdot b, \lbrace a, b \rbrace$$"]
    end

    subgraph I1["State#1"]
        direction TB
        i10["$$S' \to S \cdot, \Finv$$"]
    end

    subgraph I2["State#2"]
        direction TB
        i20["$$S \to X \cdot X, \Finv$$"] ~~~
        i21["$$X \to \cdot aX, \Finv$$"] ~~~
        i22["$$X \to \cdot b, \Finv$$"]
    end

    subgraph I3["State#3"]
        direction TB
        i30["$$X \to a \cdot X, \lbrace a, b \rbrace$$"] ~~~
        i31["$$X \to \cdot aX, \lbrace a, b \rbrace$$"] ~~~
        i32["$$X \to \cdot b, \lbrace a, b \rbrace$$"]
    end

    subgraph I4["State#4"]
        direction TB
        i40["$$X \to b \cdot, \lbrace a, b \rbrace$$"]
    end

    subgraph I5["State#5"]
        direction TB
        i50["$$S \to XX \cdot, \Finv$$"]
    end

    subgraph I6["State#6"]
        direction TB
        i60["$$X \to a \cdot X, \Finv$$"] ~~~
        i61["$$X \to \cdot aX, \Finv$$"] ~~~
        i62["$$X \to \cdot b, \Finv$$"]
    end

    subgraph I7["State#7"]
        direction TB
        i70["$$X \to b \cdot, \Finv$$"]
    end

    subgraph I8["State#8"]
        direction TB
        i80["$$X \to aX \cdot, \lbrace a, b \rbrace$$"]
    end

    subgraph I9["State#9"]
        direction TB
        i90["$$X \to aX \cdot, \Finv$$"]
    end

    I0 -->|$$a$$| I3
    I0 -->|$$b$$| I4
    I0 -->|$$S$$| I1
    I0 -->|$$X$$| I2
    
    I2 -->|$$a$$| I6
    I2 -->|$$b$$| I7
    I2 -->|$$X$$| I5

    I3 -->|$$a$$| I3
    I3 -->|$$b$$| I4
    I3 -->|$$X$$| I8

    I6 -->|$$a$$| I6
    I6 -->|$$b$$| I7
    I6 -->|$$X$$| I9

    style I1 color:#f66

    style I3 fill:#E8DAEF
    style I6 fill:#E8DAEF

    style I4 fill:#D4E6F1
    style I7 fill:#D4E6F1

    style I8 fill:#D4EFDF
    style I9 fill:#D4EFDF

“State#1” in red font represents the accept state. States with the same non-white backgraound color are mergeable by $LALR(1)$.

$LALR(1)$ 认为 State#3 + State#6、State#4 + State#7、State#8 + State#9 可以合并，于是得到：

---
config:
  layout: elk
  look: handDrawn
---
flowchart LR
    subgraph I0["State#0"]
        direction TB
        i00["$$S' \to \cdot S, \Finv$$"] ~~~
        i01["$$S \to \cdot XX, \Finv$$"] ~~~
        i02["$$X \to \cdot aX, \lbrace a, b \rbrace$$"] ~~~
        i03["$$X \to \cdot b, \lbrace a, b \rbrace$$"]
    end

    subgraph I1["State#1"]
        direction TB
        i10["$$S' \to S \cdot, \Finv$$"]
    end

    subgraph I2["State#2"]
        direction TB
        i20["$$S \to X \cdot X, \Finv$$"] ~~~
        i21["$$X \to \cdot aX, \Finv$$"] ~~~
        i22["$$X \to \cdot b, \Finv$$"]
    end

    subgraph I36["State#36"]
        direction TB
        i30["$$X \to a \cdot X, \lbrace a, b, \Finv\rbrace$$"] ~~~
        i31["$$X \to \cdot aX, \lbrace a, b, \Finv\rbrace$$"] ~~~
        i32["$$X \to \cdot b, \lbrace a, b, \Finv\rbrace$$"]
    end

    subgraph I47["State#47"]
        direction TB
        i40["$$X \to b \cdot, \lbrace a, b, \Finv\rbrace$$"]
    end

    subgraph I5["State#5"]
        direction TB
        i50["$$S \to XX \cdot, \Finv$$"]
    end

    subgraph I89["State#89"]
        direction TB
        i80["$$X \to aX \cdot, \lbrace a, b, \Finv\rbrace$$"]
    end

    I0 -->|$$a$$| I36
    I0 -->|$$b$$| I47
    I0 -->|$$S$$| I1
    I0 -->|$$X$$| I2
    
    I2 -->|$$a$$| I36
    I2 -->|$$b$$| I47
    I2 -->|$$X$$| I5

    I36 -->|$$a$$| I36
    I36 -->|$$b$$| I47
    I36 -->|$$X$$| I89

    style I1 color:#f66

    style I36 fill:#E8DAEF

    style I47 fill:#D4E6F1

    style I89 fill:#D4EFDF

合并后是有可能直接变成 $SLR(1)$ 的。

2. Conflicts Emerged after Merging / Partially $LALR(1)$?

合并 state 必然会增加 conflict 的 possibility:

• conflicting 的两个 items 如果是分开的两个 states 中的，就没事
• 一合并就必然出事

Theorem: When a conflict arises after state merging, we say the grammar is not $LALR(1)$. $\blacksquare$

按照 LR Parsing #7: LR(0) vs SLR(1) vs LR(1) - 4. The Expressive Power Perspective 的思路，有：

Grammar	Possibility of Conflicts	so a conflict-free grammar must be … structually	Expressive Power
$LR(0)$	🎲🎲🎲🎲 High	🚫🚫🚫🚫 most restrictive	👑 Low
$SLR(1)$	🎲🎲🎲	🚫🚫🚫	👑👑
$LALR(1)$	🎲🎲	🚫🚫	👑👑👑
$LR(1)$	🎲 Low	🚫 least restrictive	👑👑👑👑 High

为了避免出现 conflict，我有一个 rough 的 idea：只合并那些不会有 conflict 的 states；有 conflict 的 states 我们不合并就好了。这么一来就得到了一种 half-$LR(1)$-half-$LALR(1)$ 的形态。

学界的工作做得比我这个 rough idea 更细致，比如 $IELR(1)$，这里就不展开了。

3. Parsing Table Construction

Same with $LR(1)$’s.

4. State-Merging Algorithms

4.0 老算法改造

之前的算法 有这么几个问题：

1. $\operatorname{GOTO}^{(1)}$ 职责上稍微有点不清晰：
   • 它要负责创建新的 closure
   • 同时它又是 $T_{\operatorname{GOTO}}$ 填表的依据
2. $\text{repeat until } C \text{ is not changed}$ 没有一个具体的、高效的实现手段

我们可以这么改造一下：

\[\begin{align} &\text{// compute the canonical collection of item sets for grammar } G' \qquad \newline &\textbf{procedure } \mathrm{CC}^{(1)}(G') \text{ -> Set[Set[Item]]:} \nonumber \qquad \newline & \qquad i = [S' \to \cdot S, \Finv] \quad \text{// initial kernel item from the dummy production } \qquad \newline & \qquad I = \operatorname{CLOSURE}^{(1)}(\lbrace i \rbrace) \quad \text{// initial item set} \qquad \newline & \qquad C = \lbrace I \rbrace \quad \text{// initial canonical collection} \qquad \newline & \qquad UQ = \text{Queue(). append}(I) \quad \text{// unvisited item sets} \qquad \newline & \qquad \newline & \qquad \text{repeat until } UQ \text{ is empty} \text{: }\qquad \newline & \qquad\qquad I = UQ\text{. popleft()} \quad \text{// visiting the first item set in the queue} \qquad \newline & \qquad\qquad \text{for each symbol } X \text{: } \qquad \newline & \qquad\qquad\qquad J = \operatorname{GOTO}^{(1)}(I, X) \qquad \newline & \qquad\qquad\qquad \text{if } J = \varnothing \text{: } \qquad \newline & \qquad\qquad\qquad\qquad \text{continue} \qquad \newline & \qquad\qquad\qquad \text{if } J \not\in C \text{: } \qquad \newline & \qquad\qquad\qquad\qquad \text{// } J \text{ is not empty, and new to C} \qquad \newline & \qquad\qquad\qquad\qquad \text{// should be marked as unvisited} \qquad \newline & \qquad\qquad\qquad\qquad C\text{. add}(J) \qquad \newline & \qquad\qquad\qquad\qquad UQ\text{. append}(J) \qquad \newline & \qquad\qquad\qquad T_{\operatorname{GOTO}}[I, X] = J \qquad \newline & \qquad \text{return } C \end{align}\]

$T_{\operatorname{ACTION}}$ 填表放到 $\operatorname{CC}^{(1)}$ 结束之后再做。

4.1 Brute-Force

即在 $\operatorname{CC}^{(1)}$ 结束之后再去 scan $C$ 寻找可以合并的 item sets，而且还要去改动 $T_{\operatorname{GOTO}}$，程序写起来很麻烦。

但是如果是做练习题，这个方法还行，而且 $T_{\operatorname{GOTO}}$ 有个规律可以用：

1. 假设我们构建好了 $LR(1)$ 的 $C = \lbrace I_0, I_1, \dots, I_n \rbrace$
2. For each core $\in C$, find all item sets having that core, and compute their union, say $J_x = \bigcup \kappa_x$ where $\kappa_x = \lbrace I_i \in C \mid \operatorname{core}(I_i) = \text{the x-th core in } C\rbrace$
3. 假设 step 2 的结果是 $C’ = \lbrace J_0, J_1, \dots, J_m \rbrace$:
   • $T_{\operatorname{GOTO}} \Longrightarrow$
     • 如果 $J_p = I_i \cup \dots \cup I_k$，那么 $\forall X$, $\operatorname{GOTO}^{(1)}(I_i, X), \dots \operatorname{GOTO}^{(1)}(I_k, X)$ 也应该有相同的 core，所以你肯定能找到一个 $J_q = \operatorname{GOTO}^{(1)}(I_i, X) \cup \dots \cup \operatorname{GOTO}^{(1)}(I_k, X) \in C’$. 于是我们可以删除 $T_{\operatorname{GOTO}}(I_i, X), \dots T_{\operatorname{GOTO}}(I_k, X)$，然后添加 $T_{\operatorname{GOTO}}(J_p, X) = J_q$
       • Section 1 就是个很好的例子
     • $\forall T_{\operatorname{GOTO}}(?, ?) = I_i \text{ or } \dots \text{ or } I_k$ 都要改成 $T_{\operatorname{GOTO}}(?, ?) = J_p$
   • $T_{\operatorname{ACTION}} \Longrightarrow$ 与 $LR(1)$ 的方法一致

4.2 A simple algorithm: step-by-step merging

First described by Anderson et al. in 1973.

\[\begin{align} &\text{// compute the canonical collection of item sets for grammar } G' \qquad \newline &\textbf{procedure } \mathrm{CC\_LALR}^{(1. 1)}(G') \text{ -> Set[Set[Item]]:} \nonumber \qquad \newline & \qquad i = [S' \to \cdot S, \Finv] \quad \text{// initial kernel item from the dummy production } \qquad \newline & \qquad I = \operatorname{CLOSURE}^{(1)}(\lbrace i \rbrace) \quad \text{// initial item set} \qquad \newline & \qquad C = \lbrace I \rbrace \quad \text{// initial canonical collection} \qquad \newline & \qquad UQ = \text{Queue(). append}(I) \quad \text{// unvisited item sets} \qquad \newline & \qquad \newline & \qquad \text{repeat until } UQ \text{ is empty} \text{: }\qquad \newline & \qquad\qquad I = UQ\text{. popleft()} \quad \text{// visiting the first item set in the queue} \qquad \newline & \qquad\qquad \text{for each symbol } X \text{: } \qquad \newline & \qquad\qquad\qquad J = \operatorname{GOTO}^{(1)}(I, X) \qquad \newline & \qquad\qquad\qquad \text{if } J = \varnothing \text{: } \qquad \newline & \qquad\qquad\qquad\qquad \text{continue} \qquad \newline & \qquad\qquad\qquad \text{if } \exists K \in C \text{ such that } \operatorname{core}(K) = \operatorname{core}(J) \text{: } \quad \text{// 📌 able to merge} \qquad \newline & \qquad\qquad\qquad\qquad K' = K\text{. deep\_copy}() \qquad \newline & \qquad\qquad\qquad\qquad K' = K'\text{. merge}(J) \qquad \newline & \qquad\qquad\qquad\qquad \text{if }K = K' \text{: } \quad \text{// no change after merging} \qquad \newline & \qquad\qquad\qquad\qquad\qquad \text{continue} \quad \text{// discard } J \text{ and } K' \qquad \newline & \qquad\qquad\qquad\qquad \newline & \qquad\qquad\qquad\qquad C\text{. remove}(K) \qquad \newline & \qquad\qquad\qquad\qquad C\text{. add}(K') \qquad \newline & \qquad\qquad\qquad\qquad \text{// since it has chnged, it may lead to new and different states} \qquad \newline & \qquad\qquad\qquad\qquad UQ\text{. append}(K') \qquad \newline & \qquad\qquad\qquad\qquad \newline & \qquad\qquad\qquad\qquad T_{\operatorname{GOTO}}[I, X] = K' \qquad \newline & \qquad \text{return } C \end{align}\]

Notes on 📌:

• 你只可能找出 only one such $K$，如果有多个的话，它们理应已经被 merge 了
• 这里你可能需要一个 map(core, item_set)，查找比较方便

Cons:

• still generates almost all $LR(1)$ states (现实中 $LR(1)$ 大几千个 states 被合并成 $LALR(1)$ 几百个 states 的情况是很常见的，> 10:1 ratio)
• $K’$ 需要 revisit 的频率很高，还是有很多重复的计算

4.3 The Channel Algorithm (used by yacc)

Described in YACC: Yet Another Compiler-Compiler by Stephen C. Johnson; detailed by Aho, Sethi and Ullman in the Dragon Book.

4.3.0 Intuition: A channel is a passage in the the LR(0) NFA that carries over lookaheads (among items)

With this example grammar:

// A non-LR(0) grammar for differences of numbers
S -> E
E -> E - T
E -> T
T -> n
T -> (E)

the book Parsing Techniques constructed a NFA for it:

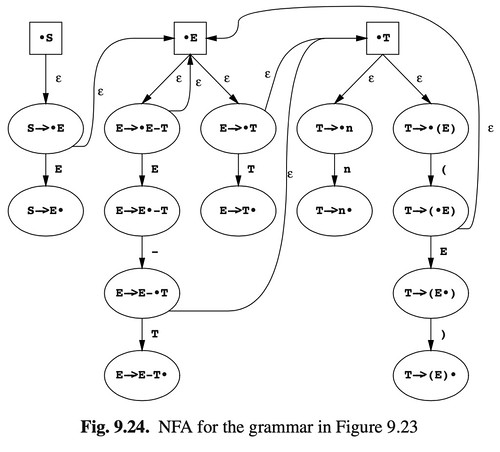
and lookaheads are carried over by two types of channels within the NFA:

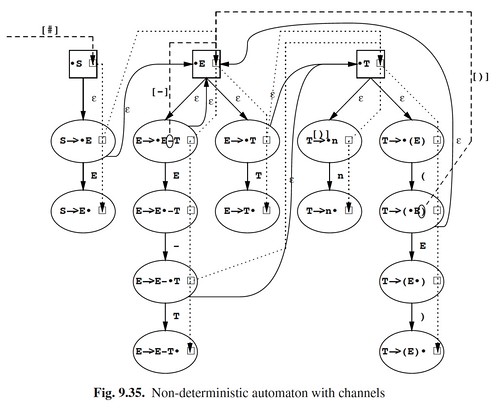
• $\square$ is like a placeholder for lookaheads
• dotted lines represent “propagated” channel
• dashed lines represent “spontaneous” channel

But in reality you don’t need to run the Channel Algorithm on NFAs like this. Actually it’s easier to work on DFAs.

The skeleton of the Channel Algorithm is like:

1. Compute all $LR(0)$ kernel items
2. Compute the lookaheads (by channels) for those kernel items, making them $LALR(1)$ kernel items
3. Expand those $LALR(1)$ kernel items into $LALR(1)$ item sets by $\operatorname{CLOSURE}^{(1)}$

4.3.1 Compute $LR(0)$ Kernel Items

Definition:

• Kernel items: the initial item $[S’ \to \cdot S]$, plus all items whose dots are not at the left end
• Non-kernel items: all other items with their dots at the left end, except for $[S’ \to \cdot S]$

$\blacksquare$

An item set may have $k > 1$ kernel items.

You can use the $\operatorname{CC}$ procedure of LR Parsing #2: Structural Encoding of LR(0) Parsing DFA to compute all $LR(0)$ items and then remove the non-kernel ones. Otherwise you can modify the procedure so that every kernel item is marked whenever it’s created.

4.3.2 Lookahead Determining Algorithm

首先我们要定义两种不同的 channel，或者说两种不同的 lookahead-attachment (to kernels) 的形式。

我强烈不建议参考 Dragon Book 的 Example 4.61 下的两个 bullet points，那根本就不是 formal definition，是针对 Example 4.61 的特殊情况的讨论。而且也不要试图去 interpret，因为你很难确定它讲的 “regardless of $a$”、”only because” 这些词是什么意思。请直接跳过去 Algorithm 4.62。

参考 Dragon Book 的 Algorithm 4.62. Let:

• $\lozenge$ be a symbol $\not \in \Sigma$.
• $I$ be an $LR(0)$ item set
• $\ker(I)$ be the set of kernel items of $I$
• $X$ be a symbol
• $\operatorname{GOTO}(I, X) = J$
• $SL : \operatorname{Set}[\operatorname{Tuple(I, \phi_i, J, \phi_j, b)}]$ is the result for “spontaneously generated lookaheads”, where:
  • $\phi_i \in \ker(I)$ is a kernel item of $I$
  • $\phi_j \in \ker(J)$ is a kernel item of $J$
  • $b$ is a lookahead symbol
  • one such entry means: lookahead $b$ is spontaneously generated by $I$ (or more specially $\phi_i$) for $\phi_j$
• $PL : \operatorname{Set}[\operatorname{Tuple(I, \phi_i, J, \phi_j)}]$ is the result for “propagated lookaheads” where:
  • one such entry means: lookaheads propagate from $\phi_i$ to $\phi_j$

Textbooks use $\#$ instead of $\lozenge$ (LaTeX \lozenge). I don’t like escaping it all the time in Markdown so I prefer $\lozenge$. This symbol is often called dummy lookahead or universal lookahead. I also would like to call it placebo lookahead.

\[\begin{align} &\text{// Algorithm 4.62: determine lookahead channels of } I \text{ on input } X \qquad \newline &\textbf{procedure } \mathrm{LAChan}(I, X) \text{:} \nonumber \qquad \newline & \qquad J = \operatorname{GOTO}^{(1)}(I, X) \qquad \newline & \qquad PL = \operatorname{Set}() \qquad \newline & \qquad SL = \operatorname{Set}() \qquad \newline & \qquad \newline & \qquad \text{for each kernel item } \phi_i = [A \to \alpha \cdot \beta] \in \ker(I) \text{: }\qquad \newline & \qquad\qquad \text{patch } \phi_i \text{ to a LALR(1) item } \phi_i' = [A \to \alpha \cdot \beta, \lozenge] \qquad \newline & \qquad\qquad \text{let } I_{\phi_i} = \operatorname{CLOSURE}^{(1)}(\lbrace \phi_i' \rbrace) \qquad \newline & \qquad \newline & \qquad\qquad \text{if } \exists \psi_i = [B \to \gamma \cdot X \delta, \lozenge] \in I_{\phi_i} \text{: } \qquad \newline & \qquad\qquad\qquad \text{// then certainly } \exists \phi_j = [B \to \gamma X \cdot \delta, \lozenge] \in J \qquad \newline & \qquad\qquad\qquad \text{let } \phi_j = [B \to \gamma X \cdot \delta, \lozenge] \qquad \newline & \qquad\qquad\qquad PL \text{ .add}(\operatorname{Tuple}(I, \phi_i, J, \phi_j)) \qquad \newline & \qquad\qquad \text{if } \exists \psi_i = [B \to \gamma \cdot X \delta, b] \in I_{\phi_i} \text{ and } b \neq \lozenge \text{: } \qquad \newline & \qquad\qquad\qquad \text{// then certainly } \exists \phi_j = [B \to \gamma X \cdot \delta, b] \in J \qquad \newline & \qquad\qquad\qquad \text{let } \phi_j = [B \to \gamma X \cdot \delta, b] \qquad \newline & \qquad\qquad\qquad SL \text{ .add}(\operatorname{Tuple}(I, \phi_i, J, \phi_j, b)) \qquad \newline & \qquad \text{return } PL, SL \end{align}\]

You don’t need to keep $X$ in the results since we know $I \overset{X}{\to} J$.

Why the dummy lookahead $\lozenge$ works? Can I replace it with some $a \in \Sigma$? 这里就涉及到了 “propagated” vs “spontaneous” 的核心问题：

如果我们是 $\phi_i = [A \to \alpha \cdot \beta, a]$ 然后找到了 $\phi_j = [B \to \gamma X \cdot \delta, b] \in J$，那么 $a \to b$ 是 “propagated” 还是 “spontaneous” 要看 “$a$ 是否决定了 $b$ 的值”。

举个例子：

• 比如说按 $\operatorname{CLOSURE}^{(1)}$，我们可能会有 $b \in \operatorname{FIRST}({\beta a})$，然后假设这个 $b$ 一路传到了 $\phi_j$ unchanged
• 此时我们能说 “$a$ 决定了 $b$ 的值” 吗？不能，因为还要继续拆：
  • 如果 $\beta$ is not nullable，那么 $b \in \operatorname{FIRST}({\beta})$，与 $a$ 无关，应该算 “spontaneous”
  • 如果 $\beta$ is nullable，那么 $b \in \operatorname{FIRST}({\beta}) \cup \lbrace a \rbrace$，与 $a$ 有关；如果最终我们得到了 $b = a$ (in $\phi_j$)，那么这应该算 “propagated”

这里就涉及了一个问题：在 $\beta$ is not nullable 时，$b \in \operatorname{FIRST}({\beta})$ 也是有可能最终得到 $b = a$ (in $\phi_j$) 的，所以你从 $b \overset{?}{=} a$ 这个关系上是无法得出 “propagated or spontaneous?” 的结论的。用 dummy lookahead $\lozenge$ 来 test 就完美解决了这个问题，因为：

• $\forall a \in \Sigma, \forall \beta \in (\Sigma \cup V)^{\ast}$, 不管你怎么操作都不会得出一个 $\lozenge \not \in \Sigma$
  • 换言之 $\lozenge$ 只可能是 “propagated”
  • 注意这里要考虑到 $I \overset{X}{\to} J$ 实际包含了 3 步：
    1. $\operatorname{CLOSURE}^{(1)}$ to get $I$
    2. shift $X$ like $[\cdot X] \to [X \cdot]$
    3. $\operatorname{CLOSURE}^{(1)}$ to get $J$
• on the other hand，如果你拿到一个 lookahead $b \neq \lozenge$，那它的值肯定不是被 $\lozenge$ 决定的，所以一定是 “spontaneous”

Special Case: $\Finv$ is “spontaneous” for $[S’ \to \cdot S]$

4.3 Construct Channel Graph

假设我们有：

---
config:
  layout: elk
  look: handDrawn
---
flowchart LR
    subgraph I["State $$\;I$$"]
        direction TB
        i0["$$\phi_i = [A \to \alpha \cdot \beta, \ell_i]$$"]
    end

    subgraph J["State $$\;J$$"]
        direction TB
        j0["$$\phi_j = [B \to \gamma X \cdot \delta, \ell_j = ?]$$"]
    end

    I -->|$$X$$| J

已知 $\ell_i$，求 $\ell_j$。我们可以初始化 $\ell_j = \varnothing$:

• 若 $(I, \phi_i, J, \phi_j) \in PL$, 则 $\ell_j \uplus \ell_i$
• 若 $(I, \phi_i, J, \phi_j, b) \in SL$, 则 $\ell_j \uplus \lbrace b \rbrace$

所以我们所有的 kernel items 构成一个 graph:

• vertex 形如 $(\phi_i, \ell_i)$
• edge 即是 $PL$
• $SL$ 可以理解成：
  • a visitor that generates lookahead $b$ when it reaches vertex $(\phi_j, \ell_j)$
  • a initializer of all $\ell$ values
    • 因为这个 graph 本质就是我们的 $LALR(1)$ DFA，所有的 edges 都已知，所以我们一开始就可以把 “spontaneous” lookaheads 都 assign 给对应的 kernel items
• $\phi_0 = [S \to \cdot S, \Finv]$ 构成 source vertex

所以剩下的工作就是根据 $PL$ edges 把所有的 $\ell$ 都填满就可以了，你用 DFS 或者 BFS 都行，但要注意这仍然是一个 fixed-point 问题，需要多次 DFS 或者 BFS 直到 $\ell$ 没有更新为止。因为：

• 你可能先处理了 $(\phi_i, \ell_i) \to (\phi_j, \ell_j)$，有 $\ell_j \uplus \ell_i$
• 但后续可能又有 $(\phi_k, \ell_k) \to (\phi_i, \ell_i)$，有 $\ell_i \uplus \ell_k$，那这个新来的 $\ell_k$ 的内容你也要更新给 $\ell_j$

Dragon Book 是用这么一个 table 来记录这个 fixed-point 的计算过程的：

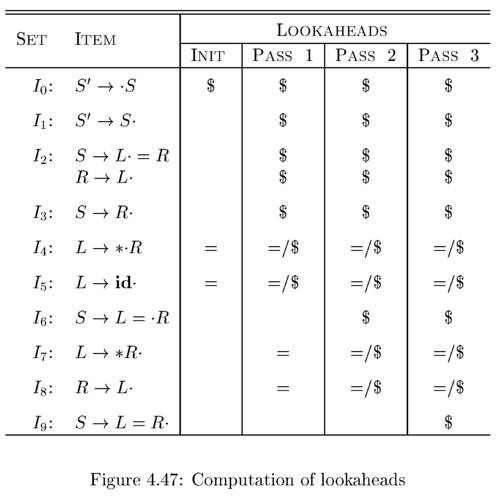
其中 INIT 就是 $SL$，后续的 PASS 就根据 $PL$ 来做。

4.4 The Relations Algorithm (Omitted)

Designed by DeRemer and Pennello (Efficient computation of LALR(1) lookahead sets).

See Section 9.7.1.3, Parsing Techniques.

4.5 LALR-by-SLR Technique (Omitted)

See Section 9.7.1.4, Parsing Techniques.