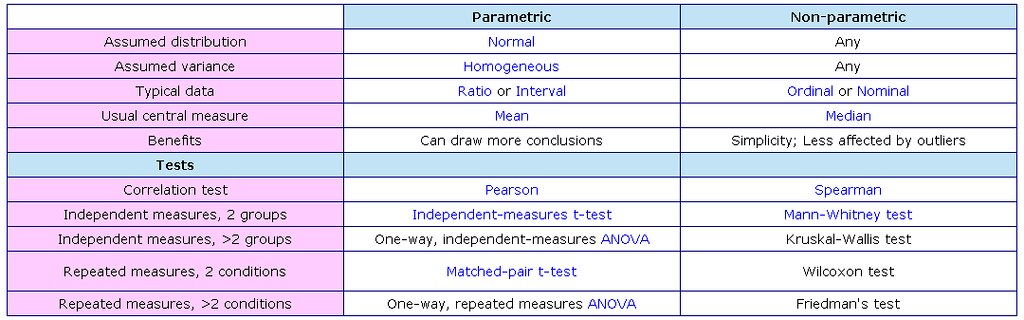
Parametric vs. non-parametric tests

参考资料：

• Handbook of Parametric and Nonparametric Statistical Procedures
• Wikipedia: Nonparametric statistics
• Parametric vs. non-parametric tests
• Levels of Measurement

---

我们先看下 Handbook 怎么说：

The inferential statistical procedures discussed in this book have been categorized as being parametric versus nonparametric tests. Some sources distinguish between parametric and nonparametric tests on the basis that parametric tests make specific assumptions with regard to one or more of the population parameters that characterize the underlying distribution(s) for which the test is employed. These same sources describe nonparametric tests as making no such assumptions about population parameters. In truth, nonparametric tests are really NOT assumption free, and in view of this some sources (e.g., Marascuilo and McSweeney (1977)) suggest that it might be more appropriate to employ the term “assumption freer” rather than nonparametric in relation to such tests.

The distinction employed in this book for categorizing a procedure as a parametric versus a nonparametric test is primarily based on the level of measurement represented by the data that are being analyzed.

• As a general rule, inferential statistical tests that evaluate categorical/nominal data and ordinal/rank-order data are categorized as nonparametric tests.
  • Categorical data and ordinal data are qualitative.
• While those tests that evaluate interval data or ratio data are categorized as parametric tests.
  • Interval and ratio data measure quantities and hence are quantitative.

关于 Qualitative / Quantitative 请参考 Statistical Data Types.

Although the appropriateness of employing level of measurement as a criterion in this context has been debated, its usage provides a reasonably simple and straightforward schema for categorization that facilitates the decision-making process for selecting an appropriate statistical test.

---