Kernel in Linear Algebra / Inner Product Space / Hyperplane / SVM / Kernel Function / Normed vector space / Metric Space

Kernel in Linear Algebra: Part 1Permalink

在 Chapter 6, Digest of Essence of Linear Algebra 有讲：

The null space of matrix $A$ is the set of all vectors $\overrightarrow{v}$ such that $A\overrightarrow{v}=\overrightarrow{0}$

这里我们用函数的观点展开讲一讲。

Wikipedia: Kernel (linear algebra): The kernel (also known as null space or nullspace) of a linear map (i.e. linear transformation) $L:V\to W$ between two vector spaces $V$ and $W$, is the set of all elements $\mathbf{v}$ of $V$ for which $L(\mathbf{v})=\mathbf{0}$, where $\mathbf{0}$ denotes the zero vector in $W$. That is, in set-builder notation,

A linear map is essentially a function，so we can define:

• $L(\mathbf{v})$ is the image of $\mathbf{v}$ in $W$ (注意有 $L(\mathbf{v})\in W$)
• The image of $L$ is $\mathrm{im}(L)=\{L(\mathbf{v})\mid \mathbf{v}\in V\}$ (所以 $\mathrm{im}(L)$ 是 $W$ 的子空间)

Two elements of $V$ have the same image in $W$ if and only if their difference lies in the kernel of $L$:

The image of $L$ is isomorphic to the quotient of $V$ by the kernel:

• In linear algebra, the quotient ([ˈkwəʊʃənt], 商) of a vector space $V$ by a subspace $N$ is a vector space obtained by “collapsing” $N$ to zero. The space obtained is called a quotient space and is denoted $V/N$ (read $V$ mod $N$ or $V$ by $N$).
• Morphism refers to a structure-preserving map from one mathematical structure to another.
  • In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations (an operation that takes a finite number of input values) and relations that are defined on it.
  • Structure 的大类有 groups (群), rings (环), fields (域，比如实数域) and vector spaces
  • 比如 Vector space 的定义就是 vector 的集合以及定义在 vector 上的 add、multiply 的操作
  • structure-preserving 的意思就是你的 mapping 不能跳出 structure 的范围
• Isomorphism is a morphism that can be reversed by an inverse morphism

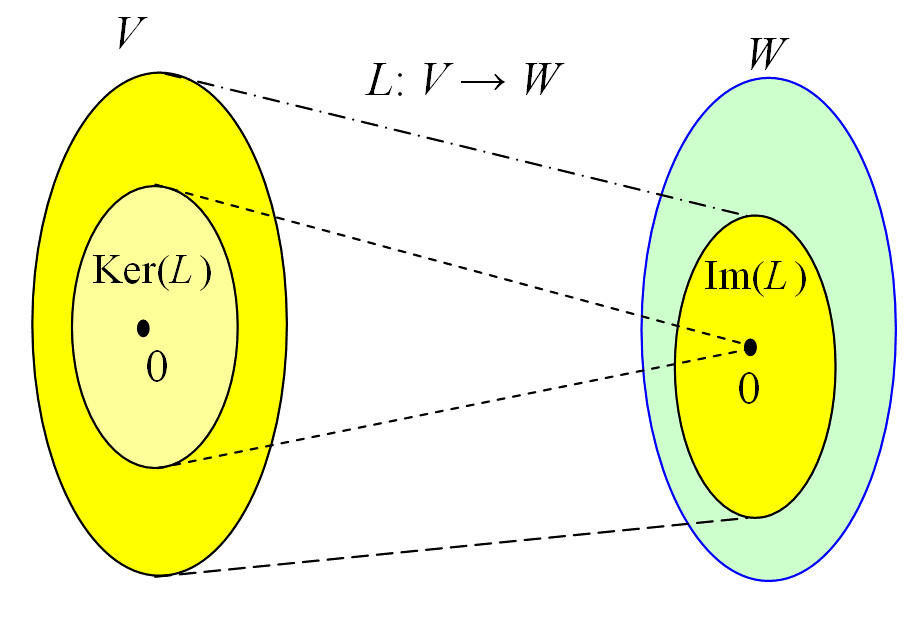
This implies the rank–nullity theorem:

where, by rank we mean the dimension of $\mathrm{im}(L)$, and by nullity that of $\ker (L)$.

• vector space 的 demension 即 basis vector 的个数

举个例子：

• $V=\{[\begin{array}{c}x\\ y\end{array}]\mid x^2+y^2=1\}$
• $W=\mathbb{R}$
• $L(\mathbf{v})=A\mathbf{v}=[\begin{array}{cc}1& 0\end{array}][\begin{array}{c}x\\ y\end{array}]=x$
  • 相当于把 $x^2+y^2=1$ 这个圆压扁到 x-axis
• $\ker (L)=\{\mathbf{v}\in V\mid \mathbf{v}=[\begin{array}{c}0\\ y\end{array}]\}$，即 y-axis 上的所有 vector
• $\mathrm{im}(L)=\{x\mid -1\le x\le 1\}$
• $\dim (\ker (L))=1,\dim (\mathrm{im}(L))=1,\dim (V)=2$

Inner Product SpacePermalink

Given a vector space $V$ on a field $K$, an inner product between the vectors $\mathbf{v}$ and $\mathbf{w}$ in $V$, which we denote by the symbol $⟨\mathbf{v},\mathbf{w}⟩$, is any operation of $V\times V\to K$ such that the following three properties are satisfied for every $\mathbf{u},\mathbf{v},\mathbf{w}\in V$ and for every $a,b\in K$:

• (Positivity or Positive Definiteness):
  • $⟨\mathbf{v},\mathbf{v}⟩\ge 0$
  • $⟨\mathbf{v},\mathbf{v}⟩=0⟺\mathbf{v}=\mathbf{0}$
• (Linearity): $⟨a\mathbf{v}+b\mathbf{v},\mathbf{w}⟩=a⟨\mathbf{u},\mathbf{w}⟩+b⟨\mathbf{v},\mathbf{w}⟩$
• (Conjugate Symmetry): $⟨\mathbf{u},\mathbf{v}⟩=⟨\mathbf{v},\mathbf{u}⟩$
  • conjugate 这个词的意义有很多，比如：
    • $x-y$ 是 $x+y$ 的 conjugate
    • $a-b\mathrm{i}$ 是 $a+b\mathrm{i}$ 的 conjugate
    • $F=Y^{-1}GY$ 是 $G$ 的 conjugate

很多地方把 inner product 这个 operation 写作 $⟨\cdot ,\cdot ⟩$，它本质就是个 function $f(\cdot ,\cdot )=⟨\cdot ,\cdot ⟩$。另外一个很烦人的地方是，inner product 你得结合语境去判断它到底是指的 $⟨\mathbf{v},\mathbf{w}⟩$ 这个具体值还是 $⟨\cdot ,\cdot ⟩$ 这个 operation。

从 inner product 的定义来看，dot product 是 inner product 的一种，即 dot product 可以通过 inner product 定义：$⟨\mathbf{v},\mathbf{w}⟩=\mathbf{v}\cdot \mathbf{w}$

我们知道 Vector space 的定义就是 vector 的集合以及定义在 vector 上的 add、multiply 的操作；如果我们在 vector space 的基础上再加上一个 $⟨\cdot ,\cdot ⟩$ 操作，我们就可以得到一个 inner product space。

Two vectors of an inner product space are orthogonal if and only if their inner product is zero.

If $V$ is an inner product space, and $W$ is a subspace of $V$, we define the orthogonal complement of $W$, which we denote by $W^{\mathrm{\perp }}$, as the set of all the vectors of $V$ that are orthogonal to every vector of $W$:

Kernel in Linear Algebra: Part 2Permalink

Let $A:V\to W$ be a linear transformation of finite-dimensional vector spaces. Then

Proof:

注意：

1. 如果有 $A:V\to W$，那么 $A^T$ 就是个 $W\to V$ 的 linear transformation
2. 这里 inner product 其实就是 dot product 了
3. 这个其实可以扩展到任意的 linear operator $A$，只是不用 $A^T$ 而是 adjoint $A^{\ast }$ 来表示逆运算

If $\mathbf{v}\in \mathrm{im}(A^T)\subset V$, then $\mathbf{v}=A^T\mathbf{w}$ for some $\mathbf{w}\in W$. Now given $\mathbf{u}\in \ker (A)$, then $A\mathbf{u}=\mathbf{0}$. Therefore,

That is $\mathbf{v}\in (\ker (A){)}^{\mathrm{\perp }}$. 后续证明暂略。感觉直接证 adjoint 更简单……

HyperplanePermalink

Let ${\mathrm{R}}^n$ be an $n$-dimension vector space and $\mathbf{a}=(a_1,a_2,\dots ,a_n)$. $\left\{a_i\right\}$ are scalars not all equal to 0. Then the set $S=\{\mathbf{x}\in {\mathrm{R}}^n\mid \mathbf{a}\cdot \mathbf{x}=b\}$, where $b$ is a constant, is a subspace of ${\mathrm{R}}^n$ called a hyperplane.

注意 $\mathbf{a}=(a_1,a_2,\dots ,a_n)$ 这个变换并没有 preserve 原点，所以它不是一个严格的 linear transformation 而是一个 affine transformation。然后 hyperplane 可以看作是这个 affine transformation $A(\mathbf{x})=\mathbf{a}\cdot \mathbf{x}-b$ 的 kernel。

Hyperplane 的 normal vector 可以由 transformation 的 gradient 给出：$\mathbf{n}=\mathrm{\nabla }A(\mathbf{x})$，刚好有 $\mathrm{\nabla }A(\mathbf{x})=\mathbf{a}$，所以 hyperplane 的 normal vector $\mathbf{n}=\mathbf{a}$

Normal vector 的性质是它垂直于 hyperplane。

对任意 vector $\mathbf{x}$，当 hyperplane 经过原点时，$\mathbf{x}$ 到 hyperplane 的距离等于它到 normal vector 的投影的绝对值，所以有：

若 hyperplane 不经过原点，我们取 hyperplane 上的任意一点 $p$，原点到 $p$ 的向量为 $\overrightarrow{op}$。我们把 $\mathbf{x}$ 写作 $\overrightarrow{ox}$，所以 $\overrightarrow{px}=\overrightarrow{ox}-\overrightarrow{op}$ 到 normal vector 的投影的绝对值才是 $\mathbf{x}$ 到 hyperplane 的距离。又因为 $p$ 在 hyperplane 上，所以 $\mathbf{a}\cdot \overrightarrow{op}=b$，所以：

注意这里有一个很重要的思想：当 hyperplane 过原点时，我们很容易错误地认为 hyperplane 是 hyperplane 上所有 vector 的集合；从 hyperplane 不经过原点的情况来看，正确的理解应该是：hyperplane 是所有从原点出发、落到 hyperplane 上的 vector 的终点的集合。扩展开来，所谓 “vector 张成的空间”，指的就是 “所有 vector 的终点所构成的空间”

造成这个误解的原因在于我混淆了 hyperplane 在几何学和集合论中的意义：

• 几何学中，hyperplane 是个平面（假设 3-D 情况下）
• 集合论中，hyperplane 是 vector 的集合（vector space）
• 我们说 vector $\mathbf{v}\in H$, where $H$ is a hyperplane，并不是说在几何学中，整个 vector $\mathbf{v}$ 都在 $H$ 这个平面之中，而是说 $\mathbf{v}$ 从原点出发，终点会落在 $H$ 这个平面之中

基于这个思想，我们还应该认识到：

1. （几何学）Hyperplane 平面上没有 vector，只有 vector 的终点；只是当 hyperplane 平面经过原点时，它恰巧包含 vector
2. （几何学）从原点出发，终点落到 hyperplane 平面上的 vector $\mathbf{x}$ 才满足 $A(\mathbf{x})=\mathbf{a}\cdot \mathbf{x}-b=0$，并不是 hyperplane 平面上的 vector 满足 $A(\mathbf{x})=\mathbf{a}\cdot \mathbf{x}-b=0$
   • （集合论）Hyperplane 这个 vector space 内的所有 vector $\mathbf{x}$ 满足 $A(\mathbf{x})=\mathbf{a}\cdot \mathbf{x}-b=0$
3. （几何学）Normal vector 垂直于 hyperplane 平面，并不是说 Normal vector 垂直于 hyperplane 平面上的所有 vector
   • （集合论）Normal vector 也并不垂直于 hyperplane 这个 vector space 内的所有 vector（除非 hyperplane 经过原点）
4. （几何学）我们可以把 原点 + hyperplane 平面 的整体结构想象成一个底面积无限大的圆锥：
   • 顶点是原点
   • 底是 hyperplane 平面
   • 顶点到底面任意一点的连线都是 vector
   • 顶点到底面几何中心的连线是一个 normal vector
     • 这个 normal vector 的长度，即圆锥的高是 $\left|\frac{b}{|\mathbf{a}|}\right|$
     • 这个 normal vector 不一定是 $\mathbf{a}$，但一定与 $\mathbf{a}$ 共线
       • 换言之 $\mathbf{a}$ 不一定落在 hyperplane 平面上
       • 再换言之 $\mathbf{a}$ 相当于是从原点出发的一个旋转臂，它的方向即圆锥高的方向
     • 已知长度和方向，我们可以得知这个 normal vector ${\mathbf{n}}^{\prime }=\left|\frac{b}{|\mathbf{a}|}\right|\frac{\mathbf{a}}{|\mathbf{a}|}=\left|\frac{b}{|\mathbf{a}{|}^2}\right|\mathbf{a}$
   • （集合论）所有顶点到底面的连线的集合构成 hyperplane 的 vector space

Affine transformation $A(\mathbf{x})=\mathbf{a}\cdot \mathbf{x}-b$ 的几何意义是：

1. 以 $\mathbf{a}$ 为 x-axis，将空间内所有 $\mathbf{x}$ 压缩到一维，即压缩到 $\mathbf{a}$ 这个 x-axis 上
2. $\mathbf{x}$ 压缩后位于 $x=\mathbf{a}\cdot \mathbf{x}$ 位置
3. 将所有压缩后的 $\mathbf{x}$ 左移 $b$
   • 此时位于 $x=0$ 位置的所有 $\mathbf{x}$ 反压缩后即是 hyperplane vector space
   • 此时原点位于 $x=-b$ 位置
   • 这个长度为 $|b|$ 的移动距离反压缩后即是圆锥的高 $\left|\frac{b}{|\mathbf{a}|}\right|$

SVMPermalink

回头看这个 SVM 的最简单的 hard-margin 就很好懂了

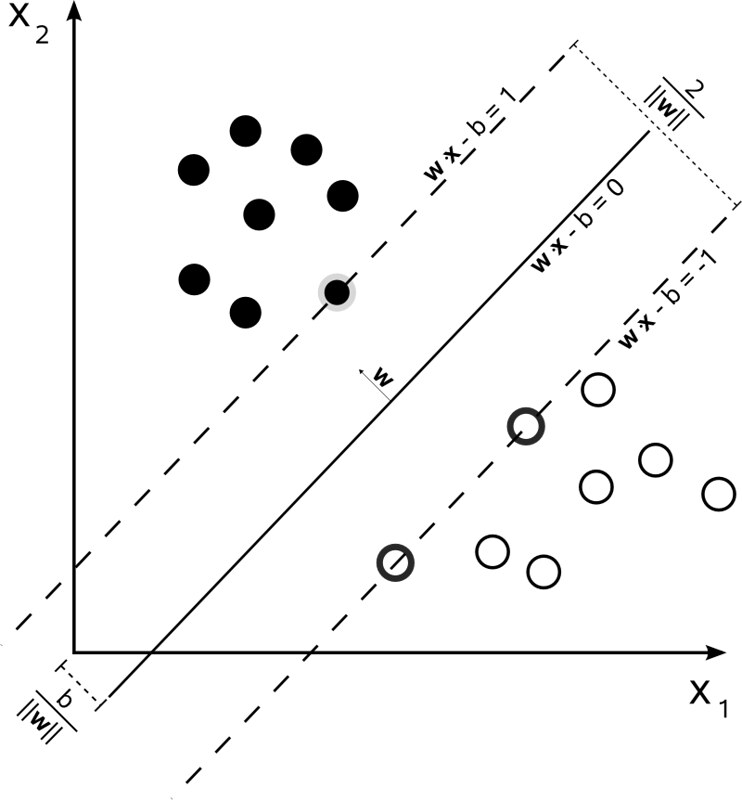
注意这个 margin 是设置成常数 1 还是符号 $c$ 并没有太大区别，因为最终都是可以通过 $|\mathbf{w}|$ 来调节的。

最终的 optimization problem:

“Minimize $|\overrightarrow{w}|$ subject to $y_i(\overrightarrow{w}\cdot {\overrightarrow{x}}_i-b)\ge 1$, for $i=1,\dots ,n$”.

这个图是 linear-separable (或者 precisely，hyperplane-separable) 的情况，如果是 non-linear-separable 的情况该怎么办呢？

用 kernel method

Kernel Method / Kernel FunctionPermalink

我们先看 Kernel Methods for Pattern Analysis 的定义：

Definition 2.8 [Kernel function] A kernel is a function $\kappa$ that for all $\mathbf{x},\mathbf{z}\in X$ satisfies

where $\varphi$ is a mapping from $X$ to an (inner product) feature space $F$

用到 SVM 里，基本思想就是：

1. 你在 vector space $X$ 不是 hyperplane 不可分嘛，我把你 transform 到另外一个 vector space $F$，如果在 $F$ 里 hyperplane 可分，problem solved
2. 我们需要用到 dot product，所以 $F$ 需要是个 inner product vector space
3. 我们其实并不关心 transformation $\varphi$ 是怎么个 transform 法，我们只关心 dot product $\varphi (x)\cdot \varphi (z)$

从定义可以看出：

• 这里 kernel 和 kernel function 是一个意思，而且和 Linear Algebra 里的 kernel 无关！（我宁愿你叫 inner-product method！）
  • How to intuitively explain what a kernel is?: Kernel is a way of computing the dot product of two vectors in some (possibly very high dimensional) feature space, which is why kernel functions are sometimes called “generalized dot product”.
• 所以凡是涉及到 inner product 的 ML 算法，应该都可以用 kernel 处理
  • 我能最快想到的场景就是 clustering，很多 metric 都可以用 inner product 表示

Normed vector space / Metric SpacePermalink

Norms and Metrics, Normed Vector Spaces and Metric Spaces: Let $V$ be a vector space. A function $|\cdot |:V\to {\mathrm{R}}_{+}$ is a norm on $V$ if it satisfies:

1. $\mathrm{\forall }\mathbf{x}\in V:|\mathbf{x}|\ge 0$
2. $\mathrm{\forall }\mathbf{x}\in V:|\mathbf{x}|=0\iff \mathbf{x}=\mathbf{0}$
3. $\mathrm{\forall }\mathbf{x},\mathbf{y}\in V:|\mathbf{x}+\mathbf{y}|\le |\mathbf{x}|+|\mathbf{y}|$
4. $\mathrm{\forall }\alpha \in \mathrm{R},\mathbf{x}\in V:|\alpha \mathbf{x}|=\alpha |\mathbf{x}|$

A vector space together with a norm is called a normed vector space.

Wikipedia: Metric space: A metric space is an ordered pair $(M,d)$ where $M$ is a set and $d$ is a metric on $M$, i.e., a function

such that for any $x,y,z\in M$, the following holds:

1. (non-negativity or separation axiom): $d(x,y)\ge 0$
2. (identity of indiscernibles): $d(x,y)=0\iff x=y$
3. (symmetry): $d(x,y)=d(y,x)$
4. (subadditivity or triangle inequality): $d(x,z)\le d(x,y)+d(y,z)$

Norms and Metrics, Normed Vector Spaces and Metric Spaces:

In other words, a normed vector space is automatically a metric space, by defining the metric in terms of the norm in the natural way. But a metric space may have no algebraic (vector) structure–i.e., it may not be a vector space–so the concept of a metric space is a generalization of the concept of a normed vector space.

所以，我们可以把 normed vector space 加上 inner product 操作，然后做成一个 inner product metric space。在这样一个 feature space 上的 clustering 应该都可以用 kernel method

更多 kernel clustering 内容参考 A Survey of Kernel Clustering Methods。