Terminology Recap: Functions

这些个术语总是见到，也总是记不住……

domain / range $\subseteq$ codomain / image (set of $f(x)$) / preimage (set of $x$)

假定有 $f: X \to Y$。

$X$ 称为 domain (domain of definition，定义域)，$Y$ 称为 codomain (上域、陪域或者到达域)

• 一般 domain 和 codomain 都是 space，但是你也可以自定义为任意的 set

image 有三个级别：

• image of an element: if $x \in X$, then $y = f(x) \in Y$ is the image of $x$ under $f$
• image of an subset: for subset $A \subseteq X$, its image under $f$ is $\lbrace f(x) \mid x \in A \rbrace$
• image of a function: $\lbrace f(x) \mid x \in X \rbrace$
  • 这个集合我们中文称值域，也有翻译成 range 的；需要注意的是：值域并不是 $Y$
  • Just forget about this translation; it’s confusing

对应的有 inverse image，或者称 preimage：

• 对 $y \in Y$, its inverse image under $f$ is $x$ such that $f(x) = y$
• 对 $S \subseteq Y$, its inverse image under $f$ is $\lbrace x \mid f(x) = y, y \in S \rbrace$
• preimage of a function 这个叫法没有意义，它其实就是 domain $X$

Injective, surjective and bijective functions

我们即可以说 $f$ is injective / surjective / bijective，也可以说 $f$ is an injection / surjection / bijection

• injective == 单射
• surjective == 满射
• bijective == 双射

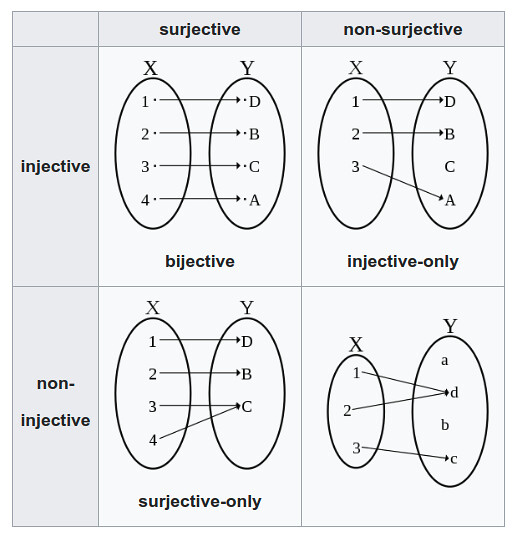
概念挺简单，我大概 15 年前就学会了，但是这三个词真的是难记，这里简单说一下：

• 这三个词的原作者，Nicolas Bourbaki，显然是把 $f: X \to Y$ 看做了一种类似 “转移” 的动作。”ject” 的原意是 “to throw”，所以 $f: X \to Y$ 大概就是 “把 $X$ 转移到另外一个集合里，这个集合我们称作 $Y$”
• injection 的话，”注入”，你联想到 “皮下注射” 的话，可以发现 这个转移的过程是没有 $X$ 的损失的，给你开了 50 ml 的药，注射到你皮下还是 50 ml
  • 如果有损失的话，那成了 “squeeze”
• surjection 的话，这个 “sur-“ 表示 “on, over”，我觉得你可以解释为 “被动“，即 “我的 $Y$ 是被 inject 进来的“，亦即存在一个 $X’ \subseteq X$ 以及一个对应的 injection，把 $X’$ inject 过来，就成了 $Y$
  • 至于 $X - X’$ 中的元素是怎么联系到 $Y$ 的，这个问题我 $X’ \leftrightarrow Y$ 的 injection 并不需要关心
• 这么一来，bijection 就好理解了：
  1. 我的 $X$ 没有损失，我有 $n$ 个 $x$ 就对应 $n$ 个 $y$
  2. 我的 $Y$ 全部来自 injection，所以不存在 $y$ 找不到 injection 的来源