Gradient Field

Gradient Field: a better way to interpret

Gradient and Directional Derivative 举了 $z = f(x,y) = 4x^2 + y^2$ 这个例子，但是举得并不好，因为它混淆了 function 的 gradient 和图形的 gradient，虽然它后面是用 level set 去解释的，相当于用平行于 $x \text{-} y$ 平面的平面去切这个椭圆抛物面，但是理解起来还是有点麻烦。

换成 Gradient Field 去理解就轻松很多。

从 gradient 的定义来看，它天生是一个 vector field。需要注意的是，我们并不需要先有一个函数 $f(x, y)$ 才能做出 vector field，只是刚好 $\nabla f(x,y)$ 是一个 vector field。

还是用 $z = f(x,y) = 4x^2 + y^2$ 的例子。

\[\newcommand{\icol}[1]{ \bigl[ \begin{smallmatrix} #1 \end{smallmatrix} \bigr] }\]

$\nabla f(x,y) = \langle 8x,2y \rangle = \icol{8x \newline 2y}$ 其实是这么一个 vector field (以下都是 Wolfram 代码)：

VectorPlot[{8x, 2y}, {x, -3, 3}, {y, -3, 3}]

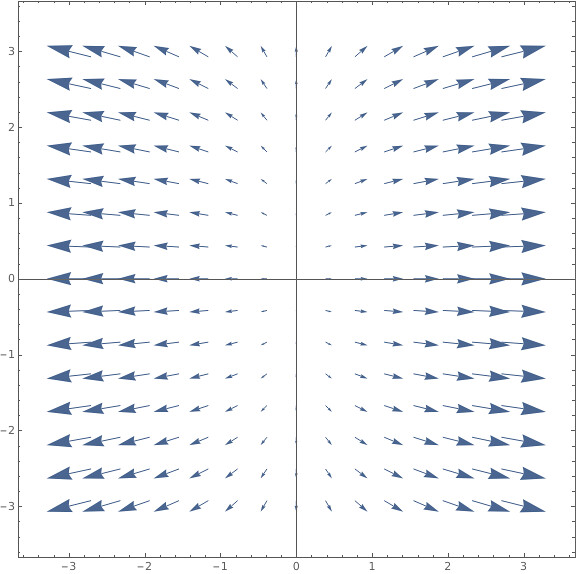
定义椭圆 $4x^2 + y^2 = c$，其实是限定了 $\nabla f(x,y) = \icol{8x \newline 2y}$ 这个函数的 domain。限定之后得到的 vector 的集合即是这个椭圆上的 gradient vectors。

考虑 3-D space 内的椭圆抛物面。这时需要把几何方程 $z = 4x^2 + y^2$ 改写成三元函数 $g(x, y, z) = 4x^2 + y^2 + 0 \cdot z$。然后 $\nabla g(x,y,z) = \langle 8x,2y,0 \rangle = \icol{8x \newline 2y \newline 0}$ 其实是这么一个 vector field:

VectorPlot3D[{8x, 2y, 0}, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}]

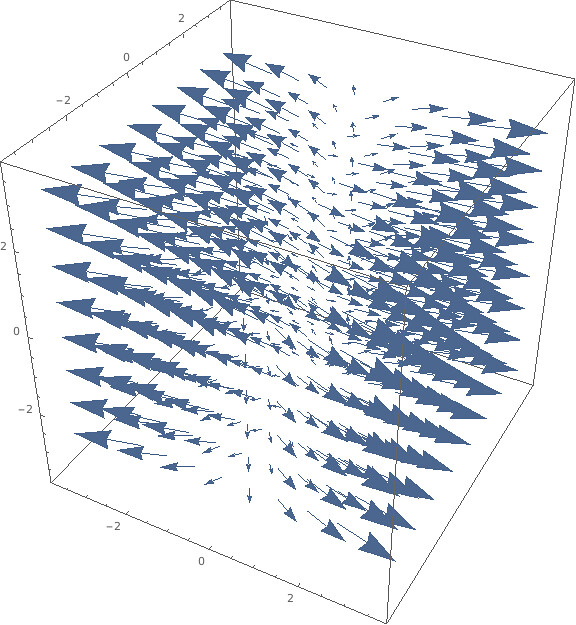
同理，定义椭圆抛物面 $4x^2 + y^2 + 0 \cdot z = c$，其实是限定了 $\nabla g(x,y,z) = \icol{8x \newline 2y \newline 0}$ 的 domain。限定之后得到的 vector 的集合即是这个椭圆抛物面上的 gradient vectors。

如果从 $z$-axis 上方看这个 vector field：

# Wolfram 类似 IPython Notebook，`%2`表示第二个 cell 的 output，即上图
Show[%2,ViewPoint->{0,0,\[Infinity]}]  

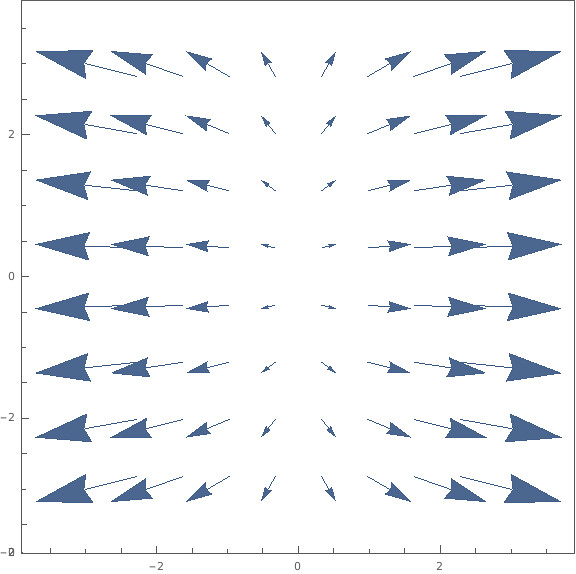
它和 $\nabla f(x,y) = \icol{8x \newline 2y}$ 其实是一样的，即你用任意的 $z=c$ 平面去截这个 3-D space，得到的平面内都是 $\nabla f(x,y)$ 这个 field。这和 level set 的解释是一样的。但是明显更好理解了。

从这个视角来看，考虑 gradient 的几何意义：gradient vector 的方向是 “the direction of steepest ascending”，即你站在 $(x,y)$ 这一点，在平面内沿 $\nabla f(x,y)$ 的方向走可以最高效地获取在椭圆抛物面 $4x^2 + y^2 + 0 \cdot z = c$ 上的 altitude，即获取更大的 $c$ 值。注意你是根据 2-D 平面上的方向去指引 3-D space 内的行动。

优化问题里用的 gradient descend 即是取 gradient vector 的反方向，进而取更小的 $c$ 值。

Clairaut’s Test

Given a vector field $\vec F(x, y) = \langle P(x, y), Q(x, y) \rangle$, how do you tell whether it’s a gradient field, i.e. $\exists G(x,y)$ such that $\nabla G = \vec F$?

Clairaut Test: if $P_y(x, y) = Q_x(x, y)$ always holds, then $\vec F(x, y) = \langle P(x, y), Q(x, y) \rangle$ is a gradient field.

Note that $P_y(x, y) = \frac{\partial P(x, y)}{\partial y}, Q_x(x, y) = \frac{\partial Q(x, y)}{\partial x}$, just a different set of notations.

Clairaut’s Test orginates from Clairaut’s theorem on equality of mixed partials:

Suppose $f$ is a real-valued function of two variables $x,y$ and $f(x,y)$ is defined on an open subset $U$ of $\mathbb{R}^2$. Suppose further that both the second-order mixed partial derivatives $f_{xy}(x,y)$ and $f_{yx}(x,y)$ exist and are continuous on $U$. Then, we have $f_{xy} = f_{yx}$ on all of $U$.

高维的情况暂不考虑；但应该类似。

Hamiltonian Vector Field

Quote from Lecture 19: Vectorfields, Math S21a: Multivariable calculus by Oliver Knill, Harvard Summer School:

If $H(x, y)$ is a function of two variables, then $\langle H_y(x, y), −H_x(x, y) \rangle$ is called a Hamiltonian Vector Field.

An example is the harmonic oscillator $H(x, y) = x^2 + y^2$. Its vector field $\langle Hy(x, y), − Hx(x, y) \rangle = \langle y, −x \rangle$.

The flow lines of a Hamiltonian vector fields are located on the level curves of $H$